栈、队
顺序
栈的顺序是始终在栈顶进行入栈和出栈操作
队的顺序是在队头进行出队,在队尾进行入队
后缀表达式
后缀表达式的转换方式
规则:从左到右遍历表达式中的每个数字和符号
若是数字直接输出,成为表达式的一部分
若是),则将栈中元素弹出并输出,直到遇到(,(弹出但不输出
若是(,+,*等符号,则从栈中弹出并输出优先级高于当前的符号,直到遇到一个优先级低的符号;然后将当前元素压入栈中
遍历结束,将栈中所有元素依次弹出,直到栈为空
后缀表达式的计算方式
若是数字直接进数字栈
若是运算符(+、-、*、/),则从符号栈中弹出两个元素进行计算(后弹出的是左运算数),并将计算结果入数字栈
遍历结束,将计算结果从数字栈中弹出。此时数字栈中应该只有一个元素,否则表达式有错
在转换中缀表达式的同时进行表达式的计算
主要思路:当一个运算符号出栈,与数据栈中的数据进行计算,计算结果依然保留在数据栈中
板子
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> typedef int DataType;int TopRank=100 ;struct NumStack { DataType data; struct NumStack *link ; }; typedef struct NumStack *NodePtrNum ;typedef struct NumStack NodeNum ;NodePtrNum TopNum=NULL ; struct OpStack { char op; int rank; struct OpStack *link ; }; typedef struct OpStack *NodePtrOp ;typedef struct OpStack NodeOp ;NodePtrOp TopOp=NULL ; void InStackNum (DataType num) { NodePtrNum q=(NodePtrNum)malloc (sizeof (NodeNum)); q->data=num;q->link=NULL ; if (TopNum==NULL ) TopNum=q; else { q->link=TopNum; TopNum=q; } } DataType OutStackNum () { DataType now=TopNum->data; TopNum=TopNum->link; return now; } void Compute (char op) { DataType now; DataType Right=OutStackNum(); DataType Left=OutStackNum(); switch (op) { case '+' :now=Left+Right;break ; case '-' :now=Left-Right;break ; case '*' :now=(DataType)(Left*Right);break ; case '/' :now=(DataType)(Left/Right);break ; } InStackNum(now); } void OpPut (char op) { int RankNow=0 ; NodePtrOp q=(NodePtrOp)malloc (sizeof (NodeOp)); q->op=op;q->link=NULL ; switch (op) { case '+' :case '-' :q->rank=RankNow=1 ;break ; case '*' :case '/' :q->rank=RankNow=2 ;break ; case '(' :q->rank=RankNow=TopRank;break ; } if (TopOp==NULL ) TopOp=q; else { if (op==')' ) { while (TopOp!=NULL &&TopOp->op!='(' ) { Compute(TopOp->op); TopOp=TopOp->link; } if (TopOp!=NULL &&TopOp->op=='(' ) TopOp=TopOp->link; } else { while (TopOp!=NULL &&TopOp->rank>=RankNow&&TopOp->rank!=TopRank) { Compute(TopOp->op); TopOp=TopOp->link; } q->link=TopOp; TopOp=q; } } } int main () { char str[100 ];gets(str); int l=strlen (str),FlagNum=0 ; double NumNow=0 ; for (int i=0 ;i<l;i++) { if (str[i]=='=' ) break ; else if (str[i]==' ' ) continue ; else if (str[i]>='0' &&str[i]<='9' ) { NumNow=(DataType)(NumNow*10 +str[i]-'0' ); FlagNum=1 ; } else { if (FlagNum) { InStackNum(NumNow); } NumNow=0 ;FlagNum=0 ; OpPut(str[i]); } } if (FlagNum) { InStackNum(NumNow); } for (NodePtrOp p=TopOp;p!=NULL ;p=p->link) { Compute(p->op); } printf ("%d" ,TopNum->data); return 0 ; }
使用数组栈实现的中缀表达式计算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> typedef double DataType;#define RankTop 100 DataType StackNum[1000 ]; char StackOp[1000 ];int TopNum=0 ,TopOp=0 ;int GetRank (char op) { int rank; switch (op) { case '+' :case '-' :rank=1 ;break ; case '*' :case '/' :rank=2 ;break ; case '(' :rank=RankTop;break ; } return rank; } void Compute (char op) { DataType Right=StackNum[--TopNum]; DataType Left=StackNum[--TopNum]; DataType Now; switch (op) { case '+' :Now=Left+Right;break ; case '-' :Now=Left+Right;break ; case '*' :Now=(DataType)(Left*Right);break ; case '/' :Now=(DataType)(Left/Right);break ; } StackNum[TopNum++]=Now; } void OpPut (char op) { if (TopOp==0 ) StackOp[TopOp++]=op; else if (op==')' ) { while (TopOp&&StackOp[TopOp-1 ]!='(' ) Compute(StackOp[--TopOp]); if (TopOp&&StackOp[TopOp-1 ]=='(' ) TopOp--; } else { while (TopOp&&StackOp[TopOp-1 ]!='(' &&GetRank(StackOp[TopOp-1 ])>=GetRank(op)) Compute(StackOp[--TopOp]); StackOp[TopOp++]=op; } } int main () { char s[200 ];gets(s); int Flag=0 ; DataType Num=0 ; for (int i=0 ;s[i]!='=' ;i++) { if (s[i]==' ' ) continue ; else if (s[i]>='0' &&s[i]<='9' ) { Num=Num*10 +s[i]-'0' ; Flag=1 ; } else { if (Flag) { StackNum[TopNum++]=Num; Num=0 ;Flag=0 ; } OpPut(s[i]); } } if (Flag) StackNum[TopNum++]=Num; while (TopOp) Compute(StackOp[--TopOp]); printf ("%.2f" ,StackNum[--TopNum]); return 0 ; }
树
基本概念
对于树,通常采用这样的方式进行表示:
本身的数据元素
第一个子节点的指针
第一个兄弟节点的指针
1 2 3 4 5 6 struct Tree { int data; struct Tree *Father ; struct Tree *Son [n ]; }
可以发现,将这样的结构进行倒置以后,呈现出树的样子
因为只有两个指针,称之为二叉树。二叉树是最基本的一种树。
相关术语
结点度
有几个子结点,称之为度
树的度
树的所有结点的度的最大值,称之为树的度
具有n个结点的非空完全二叉树的深度为h = ⌊ l o g 2 n ⌋ + 1 h=\lfloor log_2n \rfloor+1 h = ⌊ l o g 2 n ⌋ + 1
存储方式
线性存储
对于完全二叉树,可以采用数组的方式进行存储
完全二叉树可以编号
非跟结点的结点的父结点编号为i / 2 i/2 i /2
结点的左孩子为2 ∗ i 2*i 2 ∗ i 2 ∗ i + 1 2*i+1 2 ∗ i + 1
在顺序存储的二叉树中,编号为i i i j j j
链表存储:
1 2 3 4 5 6 struct TreeNode { int data; struct TreeNode *Left ; struct TreeNode *Right ; }
二叉树和树的转换
在所有的兄弟节点间添加一条连线
对于每一个结点,删除除左孩子外的所有结点
以根节点为转动中心讲树旋转45度,根节点还是原来的根节点
对于转换前后的树和二叉树,树的叶节点个数=二叉树左孩子为空的结点个数
二叉树的遍历
前序、中序、后序遍历的实质是一种深度优先算法(DFS),通常使用递归进行遍历
X序就是访问祖先结点的顺序
层次遍历是一种广度优先算法
先序遍历
访问过程:
访问根结点
先序访问其左子树
先序访问其右子树
1 2 3 4 5 6 7 8 9 void PreOrderTraversal (BinTree BT) { if (BT) { printf ("%d" ,BT->data); PreOrderTraversal(BT->Left); PreOrderTraversal(BT->Right); } }
先对左边递归,再对右边递归
中序递归
访问过程:
中序访问左子树
访问根节点
中序访问其右子树
1 2 3 4 5 6 7 8 9 void InOrderTraversal (BinTree BT) { if (BT) { IneOrderTraversal(BT->Left); printf ("%d" ,BT->data); IneOrderTraversal(BT->Right); } }
先对左边递归,再对右边递归
非递归算法的中序遍历
使用栈来保存未访问右子树的结点
采用非递归方法进行中序遍历的核心:
设置一个变量保存访问位置,初始时赋值为二叉树的根节点;设置一个栈保存遍历过程中经过但未访问的结点位置
若变量所指位置上的结点存在,则将该位置进栈,然后将变量移至左孩子
若变量所指位置上的结点不存在,则从栈中退出栈顶元素作为变量,访问该变量位置上的结点,然后将该变量移至左孩子
重复2、3过程
使用二叉树存储
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void inorder (TreePtr t) { TreePtr stack [100 ],p=t; int top=-1 ; if (t!=NULL ) { while (p!=NULL ||top!=-1 ) { for (;p!=NULL ;p=p->left) stack [++top]=p; p=stack [top--]; printf ("%d" ,p->data); p=p->right; } } }
使用数组进行存储
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void inorder (int Btree[],int n) { int stack [100 ],top=-1 ; int i=0 ; if (n>=0 ) { while (i<n||top!=-1 ) { while (i<n) { stack [++top]=i; i=i*2 +1 } i=stack [top--]; printf ("%d" ,Btree[i]); i=i*2 +2 ; } } }
后续遍历
访问过程:
后序访问其左子树
后续访问其右子树
访问根节点
1 2 3 4 5 6 7 8 9 void PostOrderTraversal (BinTree BT) { if (BT) { PosteOrderTraversal(BT->Left); PosteOrderTraversal(BT->Right); printf ("%d" ,BT->data); } }
先对左边递归,再对右边递归
表达式树
表达式树是讲后缀表达式转换为一棵二叉树,对其使用后缀遍历可以后缀表达式,中缀遍历可以得到中缀表达式
将中缀表达式转换为表达式树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> typedef double DataType;#define RankTop 100 struct tree { DataType data,num; int type; struct tree *left ,*right ; }; typedef struct tree *TreePtr ;typedef struct tree Tree ;TreePtr StackTree[100 ]; char StackOp[100 ];int TopOp=0 ,TopTree=0 ;int GetRank (char op) { int rank; switch (op) { case '+' :case '-' :rank=1 ; break ; case '*' :case '/' :rank=2 ; break ; case '(' :rank=RankTop; break ; } return rank; } void InStack (DataType data,int type) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); memset (q,0 ,sizeof (Tree)); q->data=data;q->type=type; if (type==1 ) q->num=data; else { TreePtr Right=StackTree[--TopTree]; TreePtr Left=StackTree[--TopTree]; q->left=Left;q->right=Right; switch ((char )data) { case '+' :q->num=(DataType)(Left->num+Right->num);break ; case '-' :q->num=(DataType)(Left->num-Right->num);break ; case '*' :q->num=(DataType)(Left->num*Right->num);break ; case '/' :q->num=(DataType)(Left->num/Right->num);break ; } } StackTree[TopTree++]=q; } void OpPut (char op) { if (TopOp==0 ) StackOp[TopOp++]=op; else if (op==')' ) { while (TopOp&&StackOp[TopOp-1 ]!='(' ) InStack(StackOp[--TopOp],2 ); if (TopOp&&StackOp[TopOp-1 ]=='(' ) TopOp--; } else { while (TopOp&&StackOp[TopOp-1 ]!='(' &&GetRank(StackOp[TopOp-1 ])>=GetRank(op)) InStack(StackOp[--TopOp],2 ); StackOp[TopOp++]=op; } } void Print (TreePtr p) { if (p->type==1 ) printf ("%.2f" ,(DataType)p->data); else printf ("%c" ,(char )p->data); } int main () { char s[200 ];gets(s); DataType Num=0 ;int Flag=0 ; for (int i=0 ;s[i]!='=' ;i++) { if (s[i]==' ' ) continue ; else if (s[i]>='0' &&s[i]<='9' ) { Num=(DataType)(Num*10 +s[i]-'0' ); Flag=1 ; } else { if (Flag) InStack(Num,1 ); Flag=0 ;Num=0 ; OpPut(s[i]); } } if (Flag) InStack(Num,1 ); while (TopOp) InStack(StackOp[--TopOp],2 ); TreePtr root=StackTree[--TopTree]; Print(root);printf (" " ); Print(root->left);printf (" " ); Print(root->right);printf ("\n" ); printf ("%.2f" ,root->num); return 0 ; }
递归
递归的原理实际上使用了堆栈,如何直接使用堆栈实现遍历?
中序访问的非递归遍历算法
遇到一个结点,就将其压栈,并遍历其左子树
当左子树遍历完成后,从栈顶弹出这个元素并访问之
按照其右指针再去中序遍历该结点的右子树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 typedef struct TreeNode *BinTree ;typedef BinTree Position;struct TreeNode { int data; BinTree Left; BinTree Right; } void InordeTraversal (BinTree BT) { BinTree T=BT; Stack S=CreatStack(MaxeSize); while (T||!IsEmpty(S)) { while (T) { Push(S,T); T=T->left; } if (!isEmpty(S)) { T=Pop(s); printf ("%d" ,T->data); T=T->Right; } } }
先序
中序、先序、后续的核心差别就在于根节点是什么时候打印:
中序:第二次碰到打印
先序:第一次
后续:第三次
因此只要修稿程序中打印的位置即可完成先序、后序、中序的调整
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 struct TreeNode { int data; struct TreeNode *Left ; struct TreeNode *Right ; } typedef struct TreeNode *BinTree ;void InordeTraversal (BinTree BT) { BinTree T=BT; Stack S=CreatStack(MaxeSize); while (T||!IsEmpty(S)) { while (T) { Push(S,T); T=T->left; } if (!isEmpty(S)) { T=Pop(s); T=T->Right; } } }
层序遍历
二叉树遍历的本质:将二维序列变为一维进行查找
层序遍历遵循这样的流程:
向队中存入根节点
抛出一个元素
存入该元素的左右儿子
进行2、3循环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void LevelOrderTraversal (BinTree BT) { Queue Q; BinTree T; if (!BT) return ; Q=CreateQueue(MaxSize); while (!IsEmpty(Q)) { T=Delrete(Q); printf ("%d\n" ,T->data); if (T->Left) AddQ(Q,T->Left); if (T->Right) AddQ(Q,t->Right); } }
堆栈、队列的操作中删除元素一般返回对应元素的地址
树的同构
定义:通过有限次左右子树交换可以两棵相同的树,则称之为两棵树同构
线索二叉树
利用二叉链表中空的指针域指出结点在某种遍历顺序中的直接前驱和直接后继 ,指向前驱和后继元素的指针称之为线索
利用链结点空的左指针域存放该节点的直接前驱地址,空的右节点存放直接后继地址;
非空的指针域依然存放左右孩子地址
利用rbit、lbit的值0/1代表是前驱/后继地址还是左右孩子
确定元素的直接后继
1 2 3 4 5 6 7 8 9 10 TreePtr insucc (TreePtr x) { TreePtr s=x->right; if (x->rbit==1 ) while (s->lbit==1 ) s=s->left; return s; }
建立线索二叉树
和中序遍历访问二叉树的代码基本类似,添加了建立线索的过程
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 void inThreading (TreePtr p) { if (p!=NULL ) { inThreading(p->left); if (p->left==NULL ) { p->lbit=0 ; p->left=piror; } else p->lbit=1 ; if (piror->rbit==NULL ) { piror->rbit=0 ; piror->right=p; } else piror->rbit=1 ; piror=p; inThreading(p->right); } }
线索二叉树的优点
将二叉树转变为了一个双向链表,为二叉树结点的插入、删除和查找提供了遍历
二叉查找树
二叉查找树要么是空二叉树,要么满足如下性质:
若根节点的左子树不空,则左子树上所有结点的值都小于根节点
若根节点的右子树不空,则右子树上所有结点的值都大于根节点
每一棵子树也是二叉查找树
中序遍历二叉树得到的数列为有序序列
插入结点
小于向左,大于向右
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 void insertBTree (int item) { TreePtr p=(TreePtr)malloc (sizeof (Tree)); p->data=item; p->right=p->left=NULL ; if (head==NULL ) head=p; else { TreePtr q=head; while (1 ) { if (item<q->data) { if (q->left==NULL ) {q->left=p; break ;} else q=q->left; } else if (item>=q->data) { if (q->right==NULL ) {q->right=p;break ;} else q=q->right; } } } }
查找结点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 TreePtr searchBTree (int item) { TreePtr p=head; while (p!=NULL ) { if (p->data==item) return p; else if (p->data>item) p=p->left; else if (p->data<item) p=p->right; } return NULL ; }
删除结点
先进行查找,再进行删除
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 TreePtr searchBTree (int item) { TreePtr p=head,parent=NULL ; while (p!=NULL ) { if (p->data==item) deleteBTree(p,parent); else if (p->data>item) { parent=p; p=p->left; } else if (p->data<item) { parent=p; p=p->right; } } return NULL ; } void deleteBTree (TreePtr cor,TreePtr par) { if (cor->left==NULL ) { if (cor==head) head=cor->right; else if (cor==par->left) par->left=cor->right; else par->right=cor->right; } else if (cor->right==NULL ) { if (cor==head) head=cor->left; else if (cor==par->left) par->left=cor->left; else par->right=cor->left; } else { TreePtr tar=cor->right,tarPar=cor; while (tar!=NULL ) { tarPar=tar; tar=tar->left; } cor->data=tar->data; if (tar==tarPar->left) tarPar->left=tar->right; else tarPar->right=tar->right; } }
平衡二叉树
当二叉查找树的元素单调性极好时,可能会退化成近似于链表的二叉树。引入平衡二叉树来解决这个问题:
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的,旋转分为左旋和右旋,其目的,就是减少树的高度 (哪边高,就把那边向上旋转)。
Huffman树
若给具有m个叶结点的二叉树的每个叶节点赋予一个权值,则二叉树的带权路径长度为W S L = ∑ i = 1 m w i l i WSL=\sum_{i=1}^{m}w_il_i W S L = ∑ i = 1 m w i l i w i w_i w i i i i l i l_i l i i i i
权值越大的叶结点离根结点越近,权值越小的结点离根节点越远
建立Huffman树,每次将两个最小的子树作为新书的左右孩子,再将新的树入栈
n个叶结点的Huffman树有2 n − 1 2n-1 2 n − 1
编码原理
编码需要大量使用位运算
返回一个整型变量x从第p位开始的n位
1 2 3 4 5 int getbits (int x,int p,int n) { return ((x>>p) & ~(~0 <<n)); }
基于Huffman树的加密算法
题目可以见第五次作业:树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 #include <stdio.h> #include <string.h> #include <stdlib.h> #define MAXSIZE 32 int Ccount[128 ]={0 },count=0 ; char HCode[128 ][MAXSIZE]={{0 }}; char FileOpen[MAXSIZE]={0 },FileClose[MAXSIZE]={0 };FILE *Src,*Obj; int Read (int argc,char **argv) ; struct tnode //Huffman 树结构{ char c; int weight; struct tnode *left ,*right ; }; typedef struct tnode *TreePtr ;typedef struct tnode Tree ;TreePtr Root=NULL ; void statCount () ; void createHTree () ; void makeHCode () ; void atoHZIP () ; void Zip () ; void PrintZip (char s[]) ; struct tiretree //查找树的结构{ char ch; int type; struct tiretree *right ,*left ; }; typedef struct tiretree *TTreePtr ;typedef struct tiretree TTree ;TTreePtr tHead=NULL ; TTreePtr GetTTree () ; void GetCode () ; void BuildTree () ; void Uzip () ; void GetBit (int data,char *s) ; int main (int argc,char **argv) { Read(argc,argv); Src=fopen(FileOpen,"rb" ); Obj=fopen(FileClose,"wb" ); if (argc==2 ) { statCount(); createHTree(); makeHCode(); Zip(); } else if (argc==3 ) { tHead=GetTTree(); GetCode(); BuildTree(); Uzip(); } fclose(Src); fclose(Obj); return 0 ; } int Read (int argc,char **argv) { if (argc==2 ) { if (strstr (argv[argc-1 ],".txt" )==NULL ) { printf ("File extension error!" ); return 0 ; } } else if (argc==3 ) { if (strcmp (argv[argc-2 ],"-u" )!=0 ) { printf ("Usage: hzip.exe [-u] <filename>" ); return 0 ; } if (strstr (argv[argc-1 ],".hzip" )==NULL ) { printf ("File extension error!" ); return 0 ; } } else { printf ("Usage: hzip.exe [-u] <filename>" ); return 0 ; } strcpy (FileOpen,argv[argc-1 ]); strcpy (FileClose,argv[argc-1 ]); if (argc==2 ) strcpy (FileClose+strlen (FileClose)-3 ,"hzip" ); else if (argc==3 ) strcpy (FileClose+strlen (FileClose)-4 ,"txt" ); } void statCount () { char ch; while (~fscanf (Src,"%c" ,&ch)) if (ch!='\n' ) { if (Ccount[(int )ch]==0 ) count++; Ccount[(int )ch]++; } if (Ccount[0 ]==0 ) count++; Ccount[0 ]=1 ; } struct line { TreePtr treePtr; struct line *next ; }; typedef struct line *LinePtr ;typedef struct line Line ;LinePtr head=NULL ; void InLine (TreePtr s) { LinePtr q=(LinePtr)malloc (sizeof (Line)); q->treePtr=s;q->next=NULL ; if (head==NULL ) head=q; else if ((q->treePtr->weight<head->treePtr->weight) ||(q->treePtr->weight==head->treePtr->weight &&q->treePtr->c<head->treePtr->c)) { q->next=head; head=q; } else { LinePtr p,r=NULL ; for (p=head;p!=NULL ;r=p,p=p->next) { if ((q->treePtr->weight<p->treePtr->weight) ||(q->treePtr->weight==p->treePtr->weight &&q->treePtr->c<p->treePtr->c)) { r->next=q; q->next=p; break ; } } if (p==NULL ) r->next=q; } } TreePtr OutLine () { if (head!=NULL ) { TreePtr p=head->treePtr; head=head->next; return p; } else return NULL ; } void createHTree () { for (int i=0 ;i<128 ;i++) { if (Ccount[i]) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); q->c=(char )i;q->weight=Ccount[i]; q->left=q->right=NULL ; InLine(q); } } while (head->next!=NULL ) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); q->left=OutLine();q->right=OutLine(); q->c=127 ;q->weight=q->left->weight+q->right->weight; InLine(q); } Root=OutLine(); } char key[32 ];void DFS (char ch,int cnt,TreePtr p) { if (p!=NULL ) { if (p->c==ch) { key[cnt]=0 ; strcpy (HCode[(int )ch],key); } else { if (p->right!=NULL ) { key[cnt]='1' ; DFS(ch,cnt+1 ,p->right); } if (p->left!=NULL ) { key[cnt]='0' ; DFS(ch,cnt+1 ,p->left); } } } } void makeHCode () { for (int i=0 ;i<128 ;i++) if (Ccount[i]) DFS((char )i,0 ,Root); } void PrintZip (char s[]) { int l=strlen (s),hc=0 ; char *str=(char *)malloc (l*sizeof (char )+10 ); strcpy (str,s); if (l%8 ) for (int i=0 ;i<8 -(l%8 );i++) strcat (str,"0" ); l=strlen (str); for (int i=0 ;i<l;i++) { hc=(hc<<1 )|(str[i]-'0' ); if ((i+1 )%8 ==0 ) { fputc(hc,Obj); hc=0 ; } } } void atoHZIP () { char s[10000 ],ch; memset (s,0 ,10000 ); fseek(Src,0L ,SEEK_SET); while (~fscanf (Src,"%c" ,&ch)) { strcat (s,HCode[(int )ch]); int l=strlen (s); if (l%8 ==0 ) { PrintZip(s); memset (s,0 ,10000 ); } } strcat (s,HCode[0 ]); PrintZip(s); } void Zip () { fputc(count,Obj); for (int i=0 ;i<128 ;i++) { if (Ccount[i]) { int l=strlen (HCode[i]); fputc(i,Obj);fputc(l,Obj); PrintZip(HCode[i]); } } atoHZIP(); } TTreePtr GetTTree () { TTreePtr q=(TTreePtr)malloc (sizeof (TTree)); q->ch=0 ;q->type=0 ; q->left=q->right=NULL ; return q; } void Reserve (char str[]) { int l=strlen (str); for (int i=0 ;i<l/2 ;i++) { char tmp=str[i]; str[i]=str[l-i-1 ]; str[l-i-1 ]=tmp; } } void GetBit (int data,char *s) { int x=0 ;char codeTmp[9 ]={0 }; while (data) { codeTmp[x++]=data%2 +'0' ; data/=2 ; } codeTmp[x]=0 ; int l=strlen (codeTmp); for (int i=0 ;i<8 -l;i++) strcat (codeTmp,"0" ); Reserve(codeTmp); strcat (s,codeTmp); } void GetCode () { count=(unsigned char )fgetc(Src); for (int i=0 ;i<count;i++) { int asi,len,hcode; asi=(unsigned char )fgetc(Src); len=(unsigned char )fgetc(Src); Ccount[asi]++; char code[MAXSIZE]={0 }; for (int j=0 ;j<(len/8 +1 -(len%8 ==0 ?1 :0 ));j++) { hcode=(unsigned char )fgetc(Src); if (hcode==0 ) { for (int k=0 ;k<len;k++) strcat (code,"0" ); } else GetBit(hcode,code); } code[len]=0 ; strcpy (HCode[asi],code); } } void BuildTree () { for (int i=0 ;i<128 ;i++) { if (Ccount[i]) { int l=strlen (HCode[i]); TTreePtr p=tHead; for (int j=0 ;j<l;j++) { if (HCode[i][j]=='0' ) { if (p->left==NULL ) p->left=GetTTree(); p=p->left; } else if (HCode[i][j]=='1' ) { if (p->right==NULL ) p->right=GetTTree(); p=p->right; } } p->type=1 ;p->ch=i; } } } void Uzip () { int data,pos=0 ;char code[20000 ]={0 }; TTreePtr p; while (!feof(Src)) { data=(unsigned char )fgetc(Src); GetBit(data,code); p=tHead;pos=0 ; for (int i=0 ;code[i]!=0 ;i++) { if (code[i]=='0' &&p->left!=NULL ) p=p->left; else if (code[i]=='1' &&p->right!=NULL ) p=p->right; if (p->type&&p->left==NULL &&p->right==NULL ) { if (p->ch==0 ) return ; fprintf (Obj,"%c" ,p->ch); pos=i;p=tHead; } } if (pos) { char tmp[20000 ];strcpy (tmp,code+pos+1 ); strcpy (code,tmp); } } }
图
图G的描述方式用顶点代表数据,边(弧)代表数据元素之间的关系:G = ( V , E ) G=(V,E) G = ( V , E )
概念
( v i , v j ) (v_i,v_j) ( v i , v j ) < v i , v j > <v_i,v_j> < v i , v j >
与边有关的数据称为权,边上带权的图称为网络
顶点的度
顶点的度:依附于顶点v i v_i v i T D ( v i ) TD(v_i) T D ( v i )
出度:以顶点v i v_i v i O D ( v i ) OD(v_i) O D ( v i )
入度:以顶点v i v_i v i I D ( v i ) ID(v_i) I D ( v i )
T D ( v i ) = O D ( v i ) + I D ( v i ) TD(v_i)=OD(v_i)+ID(v_i) T D ( v i ) = O D ( v i ) + I D ( v i )
对于有n个顶点,e条边的图:e = 1 2 ∑ i = 1 n T D ( v i ) e=\frac{1}{2}\sum_{i=1}^{n}{TD(v_i)} e = 2 1 ∑ i = 1 n T D ( v i )
生成树
子图
顶点、边、弧都是原图的一部分
图的连通
无向图:顶点a和顶点b之间有途径。
有向图:顶点a到b之间有路径,b到a之间也有路径
连通图:若任意两个顶点之间都有路径,则称之为连通图
连通分量 :无向图中的极大连通子图
强连通分量 :有向图中的极大连通子图
生成树
定义 :包含有n个顶点的连通图G的全部n个顶点,仅包含其中n-1条边的极小连通子图 称为G的一个生成树
边少于n-1条,则不连通;若多余n-1条,则会出现回路
一般生成树不唯一
存储方式
需要存储的信息:
所有顶点的数据信息
顶点之间的信息
权的信息(对于网络)
数组
使用两个数组:VERTS[0,1...n-1]存储顶点的数据信息,A[0,...n-1][0,...n-1]存储顶点之间的信息,将A称之为邻接矩阵
A [ i ] [ j ] = { 对于无向图 { 1 当顶点 v i 和 v j 之间有边时 0 当顶点 v i 和 v j 之间没有边时 对于带权图 { w i j 当顶点 v i 和 v j 之间有边,且边的权值为 w i j ∞ 当顶点 v i 和 v j 之间没有边时 A[i][j] =
\begin{cases}
对于无向图
\begin{cases}
1\quad \text {当顶点$v_i$和$v_j$之间有边时} \\
0\quad \text{当顶点$v_i$和$v_j$之间没有边时}\\
\end{cases}\\
对于带权图
\begin{cases}
w_{ij}\quad \text {当顶点$v_i$和$v_j$之间有边,且边的权值为$w_{ij}$} \\
\infty\quad \text{当顶点$v_i$和$v_j$之间没有边时}\\
\end{cases}\\
\end{cases}
A [ i ] [ j ] = ⎩ ⎨ ⎧ 对于无向图 { 1 当顶点 v i 和 v j 之间有边时 0 当顶点 v i 和 v j 之间没有边时 对于带权图 { w ij 当顶点 v i 和 v j 之间有边,且边的权值为 w ij ∞ 当顶点 v i 和 v j 之间没有边时
对于邻接矩阵,第i行为出度,第i列为入度
链表
对于n个顶点,设置n个头节点,第i条链表存储指向第i个结点的顶点的信息
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 typedef int DataType;struct edge { DtatType adjvex; DtatType weight; struct edge *next ; }; typedef struct edge Elink ;struct ver { DtatType vertex; Elink *link; }; typedef struct ver Vlink ;VLink G[n];
图的插入
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Elink *insertEdge (ELink *head, int avex) { ELink *e =(ELink *)malloc (sizeof (ELink)); e->adj=avex;e->wei=1 ;e->next=NULL ; if (head==NULL ) {head=e;return head;} for (ELink *p=head;p->next!=NULL ;p=p->next); p->next = e; return head; } void createGraph (VLink graph[]) { int n,v1,v2; scanf (“%d”,&n); for (int i=0 ;i<n;i++) { scanf (“%d %d”,&v1,&v2); while (v2 != -1 ) { graph[v1].link=insertEdge(graph[v1].link,v2); graph[v2].link=insertEdge(graph[v2].link,v1); scanf (“%d”,&v2); } } }
图的遍历
从某一个顶点出发,按照某一原则对所有的顶点都访问一遍
建立一个数组visited[0,...n-1],极度依托于该数组,避免出现重复访问
{ 1 表示对应的顶点已经被访问 0 表示对应的顶点还没有被访问 \begin{cases}
1 \quad 表示对应的顶点已经被访问\\
0 \quad 表示对应的顶点还没有被访问\\
\end{cases}
{ 1 表示对应的顶点已经被访问 0 表示对应的顶点还没有被访问
DFS遍历
在数据结构中,DFS指从图中某个指定的顶点v出发,先访问顶点v,然后从顶点v未被访问过的一个邻接点出发,继续进行深度优先遍历,直到图中与v相通的所有顶点都被访问;若此时图中还有未被访问过的顶点,则从另一个未被访问过的顶点出发重复上述过程,直到遍历全图。
1 2 3 4 5 6 7 8 9 10 void DFS (Vlink G[],int v) { visited[v]=1 ; for (Elink *p=G[v].link;p!=NULL ;p=p->next) if (!visited[p->adjvex]) DFS(G,p->adjvex); }
BFS遍历
在数据结构中,BFS指从图中某个指定的顶点v出发,先访问顶点v,然后依次访问顶点v的各个未被访问过的邻接点,然后又从这些邻接点出发,按照同样的规则访问它们的那些未被访问过的邻接点,如此下去,直到图中与v 相通的所有顶点都被访问;若此时图中还有未被访问过的顶点,则从另一个未被访问过的顶点出发重复上述过程,直到遍历全图。
在BFS的遍历中,需要设置一条队来方便访问。
BFS没有使用递归,而是使用了队。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 对编号为v的结点进行BFS void BFS (Vlink G[],int v) { visited[v]=1 ; InLine(head,v); while (head!=NULL ) { v=head->data; head=head->link; for (Elink *p=G[v].link;p!=NULL ;p=p->next) { if (!visited[p->adjvex]) { visited[p->adjvex]=1 ; InLine(head,p->adjvex); } } } }
BFS有些像先把下一级的结点都访问到,在从下一级开始继续;不断扩大搜索范围
独立路径计算
在这样的图中,两点之间的如今可能不止一条,使用传统的DFS或BFS可能无法解决,需要进行改进:
修改为对边进行遍历:从一个顶点对其邻接顶点进行遍历时,按邻接顶点的边进行DFS,只有当某顶点的所有边都完成遍历后才结束该顶点的遍历
我采用的方式是,对于每一个结点,在遍历相同的下一个结点的不同边时是可以做到有序的,将visited[]数组后续的分量初始化即可
(第七次作业第2题)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> #define MaxSize 100 #define Mark 114514 struct edge { int num; int weight; struct edge *next ; }; typedef struct edge Edge ;typedef struct edge *ELink ;typedef struct {VLink graph[MaxSize]; int nn,ne,cnt=0 ;int map [MaxSize],visited[MaxSize]={0 };char route[MaxSize][MaxSize];void InGraph (int tar,int num,int weight) ;void DFS (int v,int pos) ;int IfVisited (int num) ;int cmp (const void *e1,const void *e2) ;int main () { int e,d1,d2; scanf ("%d%d" ,&nn,&ne); for (int i=0 ;i<ne;i++) { scanf ("%d%d%d" ,&e,&d1,&d2); InGraph(d1,d2,e); InGraph(d2,d1,e); } DFS(0 ,0 ); qsort(route,cnt,sizeof (route[0 ]),cmp); for (int i=0 ;i<cnt;i++) { for (int j=0 ;route[i][j];j++) printf ("%d " ,route[i][j]-'0' ); printf ("\n" ); } return 0 ; } void InGraph (int tar,int num,int weight) { ELink q=(ELink)malloc (sizeof (Edge)); q->num=num;q->weight=weight; q->next=NULL ; ELink p=graph[tar].head; if (graph[tar].head==NULL ) graph[tar].head=q; else if (num<p->num) { q->next=graph[tar].head; graph[tar].head=q; } else { ELink r=NULL ; for (p=graph[tar].head;p!=NULL ;r=p,p=p->next) { if (num<p->num||(num==p->num&&weight<p->weight)) { r->next=q; q->next=p; break ; } } if (p==NULL ) r->next=q; } } void DFS (int v,int pos) { if (v==nn-1 ) { visited[v]=1 ; for (int i=0 ;i<pos;i++) route[cnt][i]=map [i]+'0' ; cnt++; } else { visited[pos]=v+Mark; for (ELink p=graph[v].head;p!=NULL ;p=p->next) { for (int i=pos+1 ;i<MaxSize;i++) visited[i]=0 ; if (!IfVisited(p->num)) { map [pos]=p->weight; DFS(p->num,pos+1 ); } } } } int IfVisited (int num) { for (int i=0 ;visited[i];i++) if (visited[i]-Mark==num) return 1 ; return 0 ; } int cmp (const void *e1,const void *e2) {return strcmp ((char *)e1,(char *)e2);}
最小生成树
定义 :包含全部n个顶点,仅包含n-1条边的极小连通子图,且总的权值之和最小
求最小生成树
若没有相同权值的边,权值最小的边一定是其最小生成树中的边
对于一个顶点,权值最小的边一定是最小生成树中的边
普里姆(Prim)法
建立两个集合G = ( V , G E ) G=(V,GE) G = ( V , GE ) T = ( U , T E ) T=(U,TE) T = ( U , TE ) v v v U = { v } , T E = ϕ , v ∈ V U=\{v\},TE=\phi,v\in V U = { v } , TE = ϕ , v ∈ V
在G中进行遍历,找到这样一条边,满足一个顶点在G中,一个在T中,且权值是符合条件最小的,将在G中的那个顶点加入T中
重复n-1次,即可得到最小连通子图
建立的数据结构:
1 2 3 4 int weight[MAX][MAX]; int edges[MAX]; int minweight[MAX];
生成的最小生成树存放在edge数组中
示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 void Prim (int weights[][MAX],int n,int src,int edges[]) { int minweight[MAX]={0 },min; int j,k; for (int i=0 ;i<n;i++) { minweight[i]=weights[src][i]; edges[i]=src; } minweight[src]=0 ; for (int i=1 ;i<n;i++) { min=INFINITY; for (j=0 ,k=0 ;j<n;j++) { if (minweight[j]!=0 &&minweight[j]<min) { min=minweight[j]; k=j; } } minweight[k]=0 ; for (j=0 ;j<n;j++) { if (minweight[j]!=0 &&weights[k][j]<minweight[j]) { minweight[j]=weights[k][j]; edges[j]=k; } } } }
Kruskal方法
对于图G = ( V , G E ) G=(V,GE) G = ( V , GE )
本质上是利用局部贪心来达到全局的最小效果
最短路径问题
定义:从A点到B点,经过的权值最小
Dijkstra算法
本质上也是一种贪心算法:对于路径中的每一个点,最短路径就是最短边+前一个点的最短路径(Spath实现的原理)
对于有n条边e个顶点的无向图,其时间复杂度为:O ( e l o g 2 e ) O(elog_2e) O ( e l o g 2 e )
数据结构:
1 2 3 4 int weight[NUM][NUM]; int spath[NUM]; int sweight[NUM]; int wfound[NUM];
Dijkstra算法:
初始化sweight[i]=weight[v0][i]
初始化sweight[v0]=0,spath[i]=v0,wfound[v0]=1
查找与v0间权重最小,且没有确定最短路径的顶点v,即在sweight[ ]中查找权重最小且没有确定最短路径的顶点
标记v为已找到最短路径的顶点
对于图G中每个从顶点v0到其最短路径还未找到,且存在边(v,w),如果从v0通过v到w的路径权值小于它当前的权值,则更新w的权值为:sweight[w]=sweight[v]+Weights[v][w]
重复3-5步n-1次
注:最短路径数组Spath含义为Spath[v]表示顶点v在最短路径上的直接前驱顶点。假设某最短路径由顶点v0,v1,v2,v3组成,则有:v2=Spath[v3],v1=Spath[v2],v0=Spath[v1]。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 #define MaxNum 100 #define INFINITY 114514 int Weights[MaxNum][MaxNum]; int Spath[MaxNum]; int Sweight[MaxNum]; char wfound[MaxNum]={0 }; int n; void Dijkstra (int v0) { int i,j,v,minweight; for (i=0 ;i<n;i++) { Sweight[i]=Weights[v0][i]; Spath[i]=v0; } Sweight[v0]=0 ; wfound[v0]=1 ; for (i=0 ;i<n-1 ;i++) { minweight=INFINITY; for (j=0 ;j<n;j++) { if (!wfound[j]&&(Sweight[j]<minweight)) { v=j; minweight=Sweight[v]; } } wfound[v]=1 ; for (j=0 ;j<n;j++) { if (!wfound[j]&&(minweight+Weights[v][j]<Sweight[j])) { Sweight[j]=minweight+Weights[v][j]; Spath[j]=v; } } } }
弊端 :不
Floyd算法
利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法
核心思想:迭代进行判断经过一个点是否会更短。
在第k次迭代中,对于( i , j ) (i,j) ( i , j ) i i i j j j A k [ i ] [ k ] = M I N { A k − 1 [ i ] [ k ] + A k − 1 [ k ] [ j ] , A k − 1 [ i ] [ j ] } A_{k}[i][k]=MIN\{A_{k-1}[i][k]+A_{k-1}[k][j],A_{k-1}[i][j]\} A k [ i ] [ k ] = M I N { A k − 1 [ i ] [ k ] + A k − 1 [ k ] [ j ] , A k − 1 [ i ] [ j ]} n − 1 n-1 n − 1
并且这样操作以后可以得到任意两个点之间的最短路径。
可以利用将权值替换为相反数得到最远路径 (较D算法的优越性)
1 2 3 4 5 6 7 8 void Floyd () { for (int k=1 ;k<=n;k++) for (int i=1 ;i<=n;i++) for (int j=1 ;j<=n;j ++) if (weight[i][k]+weight[k][j]<weight[i][j]) weight[i][j]=weight[i][k]+e[k][j]; }
AOV网
定义 :以顶点表示活动,以有向边表示活动之间的优先关系
拓扑排序
拓扑排序:若有向图G = ( V , E ) G=(V,E) G = ( V , E ) 有向图 ,V中点点v 1 , v 2 . . . v n v_1,v_2...v_n v 1 , v 2 ... v n
AOV网是否能够进行:无回路 则可以顺利进行(不会a优于b且b优于a的矛盾情况)
为了判断AOV网是否能够进行,需要进行拓扑排序(由某个几何上的一个偏序得到该集合上一个全序的操作)
方法(判断是否有回路):
在AOV网中任意选择一个没有前驱(入度为0)的结点
在AOV网中取代哦该系欸但以及从该节点为顶点出发的所有边
重复这个过程,直到所有顶点都被去除
自然语言:
建立一个栈,将所有入度为0的点入栈
当栈不为空时:
从栈中弹出一个顶点
从AOV网中删去该顶点以及从该顶点出发的边
若此时边的另一顶点入度为0,则将该顶点入栈
若还有顶点,则有回路;反之无回路
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 int dot[100 ],top=-1 ;void Delete (int p) { G[p].link=NULL ; for (int i=0 ;i<n;i++) { Elink *q,*r=NULL ; for (*q=G[i].link;q!=NULL ;r=p,q=q->next) { if (q->adjvex==p) { r->next=q->next; G[q->adjvex].In--; } } if (G[i].In==0 ) { dot[++top]=i; Delete(i); } } } int IfGood (int n) { for (int i=0 ;i<n;i++) if (G[i].In==0 ) dot[++top]=i; while (top!=-1 ) { int p=dot[top--]; Delete(p); } int flag=1 ; for (int i=0 ;i<n;i++) if (G[i].link!=NULL ) flag=0 ; if (flag) printf ("good" ); else printf ("bad" ); }
或者进行DFS:若从某一个结点出发能够回到自己,说明有回路
AOE网
相较于AOV网,AOE网的边上有代表时间的权值,关心活动的开始和结束时间
正常情况下,AOE网中只有一个入度为0的点,称之为源点,只有一个出度为0的点,称之为终点。
工程什么时候开始
进入某时间所有边代表的时间都完成后,才能进行该顶点代表的事件
关键路径 :从源点到重点的路径中路径长度最大的一条,关键路径上的活动称为关键活动
关键路径的长度为完成整个工程的最短时间 (最长的路径反而是最短时间)
某事件是否为关键时间:最早开始时间ee是否等于最晚开始时间le
计算最早时间ee
e e [ k ] = { 0 , k = 0 M A X { e e [ j ] + ( j , k ) 的权 } , k 为 j 的后继结点 ee[k]=
\begin{cases}
0 \quad ,k=0\\
MAX \{ee[j]+(j,k)的权 \} \quad, k为j的后继结点
\end{cases}
ee [ k ] = { 0 , k = 0 M A X { ee [ j ] + ( j , k ) 的权 } , k 为 j 的后继结点
计算最晚时间le
不影响这个活动的情况下,事件k最晚发生的时间:建立在关键路径的基础上
确定结点i i i l e le l e i i i j j j e e ee ee
l e [ i ] = { e e [ n − 1 ] i = n − 1 M I N { l e [ j ] − ( i , j ) 的权 } , j 为 i 的后继结点 le[i]=
\begin{cases}
ee[n-1] \quad i=n-1\\
MIN\{le[j]-(i,j)的权\} \quad ,j为i的后继结点
\end{cases}
l e [ i ] = { ee [ n − 1 ] i = n − 1 M I N { l e [ j ] − ( i , j ) 的权 } , j 为 i 的后继结点
流量计算问题
算法设有3个图(原图G、流图Gf、残余图Gr),在其上分阶段进行。Gf表示在算法的任意阶段已经达到的流,算法终止时其包含最大流; Gr称为残余图(residual graph),它表示每条边还能再添加上多少流(即还残余多少流),对于Gr中每条边(称为残余边,residual edge)可以从其容量中减去当前流来计算其残余流。
初始时Gf所有边都没有流(流为0),Gr与G相同;
每个阶段,先从Gr中找一条从s到t的路径(称为增长路径augmenting path)
将该路径上最小边的流量作为整个路径的流(权),并将路径加至流图Gf中;
将该权值路径从Gr中减去,若某条边权值为0,则从Gr中除去;
将具有该权的反向路径加到Gr中;
重新执行步骤2,直到Gr中无从s到t的路径;
将Gf中顶点t的每条入边流值相加得到最大流。
查找
查找表:记录呈现在用户眼前的排列的先后次序关系(线性结构)
有序:逻辑结构
连续:存储结构
排序文件在存储介质上采用连续组织方式:有序连续顺序表
平均查找长度ASL :确定一个记录在查找表中的位置所需要进行关键字值的比较次数的期望值/平均值
A S L ASL A S L p i p_i p i i i i c i c_i c i i i i
只有散列查找法的ASL与元素个数n无关
折半查找
平均查找长度A S L = n + 1 n l o g 2 ( n + 1 ) − 1 ASL=\frac{n+1}{n}log_2(n+1)-1 A S L = n n + 1 l o g 2 ( n + 1 ) − 1
条件:数据元素按值有序排列,采用顺序存储结构
非递归版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 typedef int DataType;int midSearch (DataType key[],int n,DataType k) { int low=0 ,high=n-1 ,mid; while (low<=high) { mid=(low+high)/2 ; if (k==key[mid]) return mid; else if (k>key[mid]) low=mid+1 ; else if (k<key[mid]) high=mid-1 ; } return low; }
递归版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 typedef int DataType;int midSearch (DataType key[],int n,DataType k) { int low=0 ,high=n-1 ,mid; while (low<=high) { mid=(low+high)/2 ; if (k==key[mid]) return mid; else if (k>key[mid]) midSearch(key,low,mid-1 ,k); else if (k<key[mid]) midSearch(key,mid+1 ,high,k); } return low; }
索引
索引:记录关键字值于记录的存储位置之间的对应关系
稠密索引:基本数据中的每一个记录在索引表中都有一项
非稠密索引(分块索引):将文件中的基本数据分为若干块,索引表为每一块建立一项
块与块之间按照关键字值有序,块内不一定
先查找索引表(确定所在块),再在块中查找
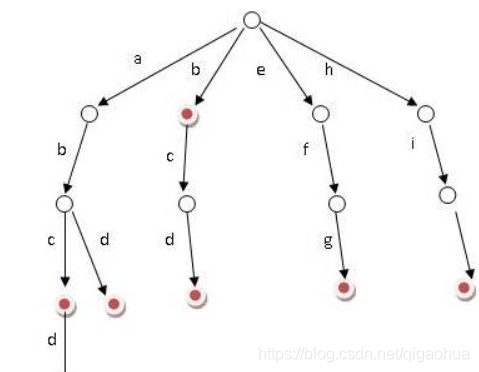
Tire树
Tire树用于存储字典,统计词频信息。其基本结构是一颗多叉树,每一个结点统计如下信息:
本身代表了所存储的字符(不是字符串),是字符
是单词的一部分还是单词的结尾,是否为叶结点
26个指针,指向下一个字符,可以根据字符的种类调整数量
Tire树的长度取决于单词的最大长度
基本结点形式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 struct tire { int count; struct tire *next [26]; }; typedef struct tire *TreePtr ;typedef struct tire Tree ;TreePtr CreateLeaf () { TreePtr q=(TreePtr)malloc (sizeof (Tree)); memset (q,0 ,sizeof (Tree)); return q; } void BuildTire (TreePtr root,char word[]) { TreePtr p=root; for (int i=0 ;word[i];i++) { int pos=word[i]-'a' ; if (p->next[pos]==NULL ) p->next[pos]=GetLeaf(); p=p->next[pos]; } p->count++; }
B树
多路查找树,基本结点为:基本数据+索引表
B树是B-树,这是一个翻译问题(B-树就是B树,不是B减树,而是B杠树,中文通常称为B树,英语称为B-tree. )
B-树
一棵m阶B-树满足如下要求:
每个分支结点最多有m课子树,最多有m-1个关键数
除根节点外,每个分支结点最少有2棵子树(不小于的最小整数)
根节点最少有两个子树(若同时为叶节点,则整棵树只有一个结点)
所有的叶节点都在同一层上,不包含任何关键字信息
每个结点包含:
数量n,代表含有n+1课子树
关键字key,共有n个,且满足k e y i < k e y i + 1 key_i<key_{i+1} k e y i < k e y i + 1
指向第i+1棵子树的指针p i p_i p i
p i p_i p i k e y i key_i k e y i k e y i + 1 key_{i+1} k e y i + 1
处于查找效率考虑,一般要求m>=3
B-树的查找
先查找该结点的关键字,若相等查找成功,key小于key[ i ] 则进入ptr[ i-1 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #define M 1000 #define MaxKey 114514 typedef int DataType;struct node { int keynum; DataType key[M+1 ]; struct node *ptr [M +1]; }; typedef struct node *BNodePtr ;typedef struct node BNode ;DataType searchBtree (BNodePtr t,DataType k) { int i,n; BNodePtr p=t; while (p!=NULL ) { n=p->keynum; p->key[n+1 ]=MaxKey; i=1 ; while (k>p->key[i]) i++; if (k==p->key[i]) return p->key[i]; else p=p->ptr[i-1 ]; } return -1 ; }
B-树的插入
新关键字总是插在叶子结点上
若将k插入到某结点后使得该结点中关键字值数目超过m-1时,则要以该结点位置居中的那个关键字值为界将该结点一分为二,产生一个新结点,并把位置居中的那个关键字值插入到双亲结点中;如双亲结点也出现上述情况,则需要再次进行分裂.最坏情况下,需要一直分裂到根结点,以致于使得B-树的深度加1。
从这样的拆分过程可以看出,B-树是一种自平衡的树
B+树
一棵m阶B+树满足如下要求:
每个分支结点最多有m课子树
除根节点外,每个分支结点最少有{m/2}课子树(不小于的最小整数)
根节点最少有两个子树(若同时为叶节点,则整棵树只有一个结点)
具有n棵子树的结点一定有n个关键字
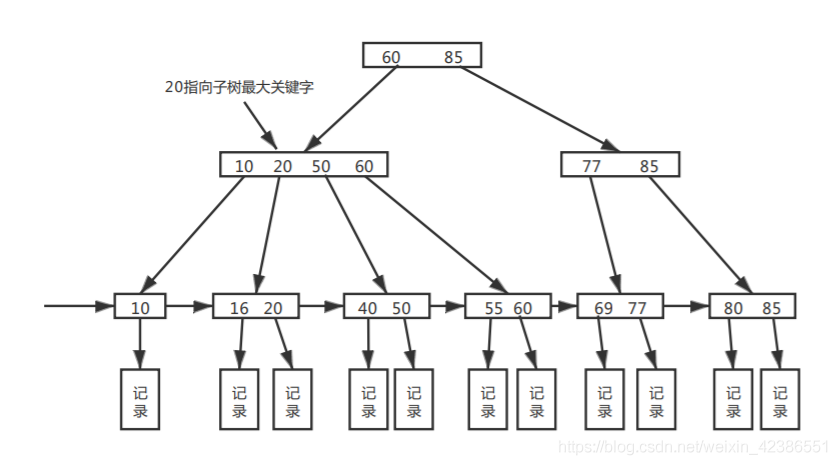
叶结点中存放记录的关键字以及指向记录 的指针,或者数据分块后每块的最大关键字值及指向该块的指针 ,并且叶结点按关键字值的大小顺序链接成线性链表
所有分支结点可以看成是索引的索引,结点中仅包含它的各个孩子结点中最大(或最小)关键字值和指向孩子结点的指针
B+树和B-树的区别(重要)
B-树的每个分支结点中含有该结点中关键字值的个数,B+树没有
B-树的每个分支结点中含有指向关键字值对应记录的指针,而B+树只有叶节点有指向关键字值对应记录的指针
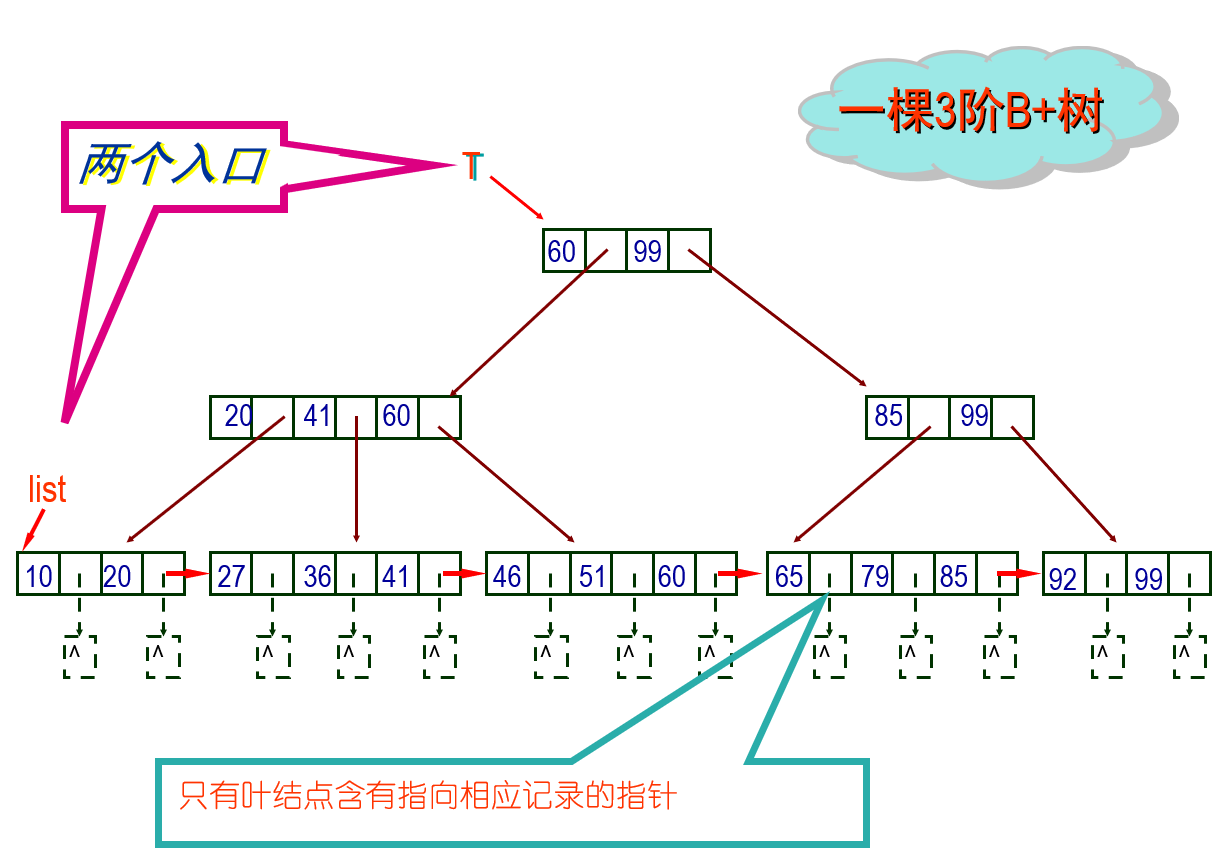
B-树只有一个指向根节点的入口,而B+树的叶结点被练成一个链表,因而B+树有两个入口,一个指向根节点,一个指向最小关键字所在的叶节点
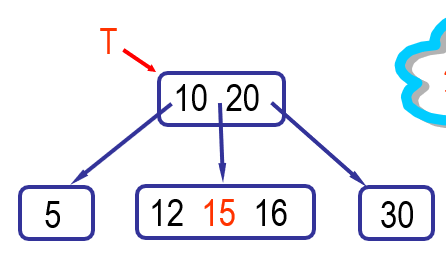
3的一个简单图示:
在B+树中,叶结点包含信息,所有非叶结点仅起到索引作用,非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针,不含该关键字对应记录的存储地址。
在B+树中,叶结点包含了全部关键字,即在非叶结点中出现的关键字也会出现在叶结点中;而在B树中,叶节点包含的关键字和其他结点包含的关键字是不重复的。 **
散列查找
散列查找即为经常听到的哈希查找,将关键字进行计算得到哈希函数(散列函数)A = H ( k ) A=H(k) A = H ( k )
散列表是根据构造的散列函数将一组关键字映射到一个有限的连续地址集合上
常见的散列函数:
直接定值法:H ( k ) = a k + b H(k)=ak+b H ( k ) = ak + b
数字分析法
平方取中法
叠加法
级数转换法
除留余数法:H ( k ) = k m o d p H(k)=kmodp H ( k ) = km o d p
处理散列冲突的方法
散列冲突:不同的关键字用同一个关键字
开放地址法
向散列中“空”地址向处理冲突开放D i = ( H ( k ) + d i ) M O D m , i = 1 , 2 , 3... D_i=(H(k)+d_i)MODm,i=1,2,3... D i = ( H ( k ) + d i ) MO D m , i = 1 , 2 , 3...
其中H ( k ) H(k) H ( k ) m m m d i d_i d i
线性探测再散列:d i = 1 , 2 , 3... m − 1 d_i=1,2,3...m-1 d i = 1 , 2 , 3... m − 1
二次探测再散列:d i = 1 2 , − 1 2 , 2 2 , − 2 2 . . . d_i=1^2,-1^2,2^2,-2^2... d i = 1 2 , − 1 2 , 2 2 , − 2 2 ...
伪随机再散列:d i = d_i= d i =
再散列法
D i = H i ( k ) D_i=H_i(k) D i = H i ( k ) D i D_i D i H i ( k ) H_i(k) H i ( k )
链地址法
将所有散列地址相同的记录连接成一个线性链表,用bucket[0....m-1]分别存放m个链表的头指针
新插入的元素放在链表的头部,这样效率更高
也可以使用二叉查找树或另一个散列表代替链表来提高查找效率
排序
排序的目的:提高查找效率
排序的评价标准:
时间性能(时间复杂度按照最差情况考虑)
空间性能(所需要的额外辅助空间)
稳定性(值相同的两个元素,排序前后相对位置是否改变)
简单算法:冒泡、选择、插入
改进算法:谢尔、堆、归并、快速
从时间复杂度来看:
平均情况:后3种改进算法 > 谢尔 (远)> 简单算法
最好情况:冒泡和插入排序要更好一些
最坏情况:堆和归并排序要好于快速排序及简单排序
从空间复杂度来看:
归并排序有额外空间要求,快速排序也有相应空间要求,堆排序则基本没有。
从稳定性来看:
除了简单排序,归并排序不仅速度快,而且还稳定
冒泡排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void BubbleSort () { int i,j,flag=1 ; for (i=n-1 ;i>0 &&flag==1 ;i--) { flag=0 ; for (j=0 ;j<i;j++) if (num[j]>num[j+1 ]) { swap(&num[j],&num[j+1 ]); flag=1 ; } } }
选择排序
1 2 3 4 5 6 7 8 9 10 11 12 13 void MinSort () { int i,j,d; for (i=0 ;i<n-1 ;i++) { d=i; for (j=i+1 ;j<n;j++) if (num[j]<num[d]) d=j; if (d!=i) swap(&num[d],&num[i]); } }
插入排序
1 2 3 4 5 6 7 8 9 10 11 12 13 void InsertSort (DataType k[],int n) { int i,j; DataType temp; for (i=1 ;i<n;i++) { temp=k[i]; for (j=i-1 ;j>=0 &&temp<k[j];j--) k[j+1 ]=k[j]; k[j+1 ]=temp; } }
折半插入排序法
节省了比较次数,但移位依然是n-1次,时间复杂度O ( n 2 ) O(n^2) O ( n 2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 void InsertBSort (DataType k[],int n) { int i,j,low,high,mid; DataType temp; for (i=1 ;i<n;i++) { temp=k[i]; low=0 ;high=i-1 ; while (low<=high) { mid=(low+high)/2 ; if (temp<k[mid]) high=mid-1 ; else low=mid+1 ; } for (j=i-1 ;j>=0 ;j--) k[j+1 ]=k[j]; k[j+1 ]=temp; } }
堆排序
堆排序是不稳定的排序,空间复杂度为O ( 1 ) O(1) O ( 1 ) O ( n l o g n ) O(nlogn) O ( n l o g n ) O ( n l o g n ) O(nlogn) O ( n l o g n )
堆的定义 :
n个元素的序列,满足k i > = k 2 i , k i > = k 2 i + 1 k_i>=k_{2i},k_i>=k_{2i+1} k i >= k 2 i , k i >= k 2 i + 1 k i < = k 2 i , k i < = k 2 i + 1 k_i<=k_{2i},k_i<=k_{2i+1} k i <= k 2 i , k i <= k 2 i + 1 i i i k i > = k 2 i + 1 , k i > = k 2 i + 2 k_i>=k_{2i+1},k_i>=k_{2i+2} k i >= k 2 i + 1 , k i >= k 2 i + 2
一棵完全二叉树,任何一个几点的值都大于孩子结点的值
排序过程
将原始序列转换为一个堆
将堆的第一个元素和最后一个元素交换(第一个元素是最大的元素)
将1~n-1(即到刚刚的交换的最大元素)组成的子序列重新转换成一个堆
重复2-3步n-1次
转换成堆的过程:
从最后一棵子树开始,向前调整
自底向上进行调整
如果父节点小于两个孩子结点中的较大值,则交换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 typedef int keytype;void adjust (keytype k[],int i,int n) { int j=2 *i+1 ; keytype temp=k[i]; while (j<n) { if (j+1 <n&&k[j]<k[j+1 ]) j++; if (temp>=k[j]) break ; k[i]=k[j]; i=j;j=2 *i+1 ; } k[i]=temp; } void heapSort (keytype k[ ],int n) { int i; keytype temp; for (i=n/2 -1 ;i>=0 ;i--) adjust(k,i,n); for (i=n-1 ;i>=1 ;i--) { temp=k[i];k[i]=k[0 ];k[0 ]=temp; adjust(k,0 ,i); } }
归并排序
将两个相邻、各自按值有序的子序列合并成一个有序的序列
对于整个序列,从有短到长的序列进行合并
本质上是一种分治算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 void merge (int tmp[],int left,int leftend,int rightend) { int i=left,j=leftend+1 ,q=left; while (i<=leftend&&j<=rightend) if (num[i]<=num[j]) tmp[q++]=num[i++]; else tmp[q++]=num[j++]; while (i<=leftend) tmp[q++]=num[i++]; while (j<=rightend) tmp[q++]=num[j++]; for (i=left;i<=rightend;i++) num[i]=tmp[i]; } void mSort (int tmp[],int left,int right) { int center; if (left<right) { center=(left+right)/2 ; mSort(tmp,left,center); mSort(tmp,center+1 ,right); merge(tmp,left,center,right); } } void BinSort () { int *tmp=(int *)malloc (sizeof (int )*n); mSort(tmp,0 ,n-1 ); }
快排qsort
从当前参加排序的元素中任选一个元素(通常称之为分界元素pivot),与当前参加排序的那些元素进行比较,凡是小于分界元素的元素都移到分界元素的前面,凡是大于分界元的元素都移到分界元素的后面,分界元素将当前参加排序的元素分成前后两部分,而分界元素处在排序的最终位置 。
只要是符合将元素按分界元素划分的算法都是快排,选择分解元素的方式有很多种
然后,分别对这两部分中大小大于1的部分重复上述过程,直到排序结束。
每次排序至少可以确定一个元素的最终位置
快排是不稳定的
原理
反复执行动作i + + i++ i + + K [ s ] < K [ i ] K[s]<K[i] K [ s ] < K [ i ] i = t i=t i = t
反复执行动作j − − j-- j − − K [ s ] > K [ j ] K[s]>K[j] K [ s ] > K [ j ] j = s j=s j = s
若i < j i<j i < j K [ i ] K[i] K [ i ] K [ j ] K[j] K [ j ]
若i < j i<j i < j K [ s ] K[s] K [ s ] K [ j ] K[j] K [ j ] K [ s ] K[s] K [ s ] K [ s ] K[s] K [ s ]
l e f t left l e f t
r i g h t right r i g h t n − 1 n-1 n − 1
i , j i, j i , j l e f t left l e f t r i g h t + 1 right+1 r i g h t + 1
K [ s ] K[s] K [ s ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 typedef int keytype;void swap (int *p,int *q) { int a=*p; *p=*q;*q=a; } void QuickSort (int left,int right) { int i,last; if (left<right) { last=left; for (i=left+1 ;i<=right;i++) if (num[i]<num[left]) swap(&num[++last],&num[i]); swap(&num[left],&num[last]); QuickSort(left,last-1 ); QuickSort(last+1 ,right); } }
桶排序
假设a 1 , a 2 , . . . . a n a_1,a_2,....a_n a 1 , a 2 , .... a n
1 2 3 4 5 6 7 void bucketSort (int k[],int n) { int c[M]={0 },i,j; for (i<0 ;i<n;i++) c[k[i]]++; for (i=0 ;i<m;i++) if (c[i]) k[j++]=i; }
最快的排序算法,O ( m + n ) O(m+n) O ( m + n )
往年题狂刷
2018
学生在线上机时间统计
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct node { char name[25 ]; long long id; int time; }stu[100 ]; int cmp (const void *e1,const void *e2) { struct node *p =struct node *)e1; struct node *q =struct node *)e2; if (p->time==q->time) return (p->id<q->id)?-1 :1 ; else return (p->time<q->time)?-1 :1 ; } int main () { freopen("a.in" ,"r" ,stdin ); freopen("a.out" ,"w" ,stdout ); char name[25 ]; long long id; int time,now=0 ; int n;scanf ("%d\n" ,&n); for (int i=0 ;i<n;i++) { int flag=1 ; scanf ("%s %lld %d" ,name,&id,&time); for (int j=0 ;j<now;j++) { if (stu[j].id==id) { stu[j].time+=time; flag=0 ; break ; } } if (flag) { strcpy (stu[now].name,name); stu[now].time=time; stu[now].id=id; now++; } } qsort(stu,now,sizeof (stu[0 ]),cmp); for (int i=0 ;i<now;i++) printf ("%s %lld %d\n" ,stu[i].name,stu[i].id,stu[i].time); return 0 ; }
后缀表达式计算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> typedef double DataType;struct tree { DataType data,num; char type,code[100 ]; struct tree *left ,*right ; }; typedef struct tree *TreePtr ;typedef struct tree Tree ;TreePtr StackTree[100 ]; int TopTree=0 ;void InStack (DataType data,char type) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); memset (q,0 ,sizeof (Tree)); q->type=type;q->data=data; if (type==1 ) q->num=data; else { TreePtr Right=StackTree[--TopTree]; TreePtr Left=StackTree[--TopTree]; q->left=Left;q->right=Right; switch ((char )data) { case '+' :q->num=(DataType)(Left->num+Right->num);break ; case '-' :q->num=(DataType)(Left->num-Right->num);break ; case '*' :q->num=(DataType)(Left->num*Right->num);break ; case '/' :q->num=(DataType)(Left->num/Right->num);break ; } } StackTree[TopTree++]=q; } int GetRank (DataType op) { int rank; switch ((char )op) { case '+' :case '-' :rank=1 ;break ; case '*' :case '/' :rank=2 ;break ; } return rank; } void DFS (TreePtr p) { if (p!=NULL ) { DFS(p->left); DFS(p->right); char *str=p->code; if (p->type==2 ) { if (p->left->type==2 &&GetRank(p->left->data)<GetRank(p->data)) { str[0 ]='(' ; strcat (str,p->left->code); str[strlen (str)]=')' ; } else strcpy (str,p->left->code); str[strlen (str)]=(char )p->data; if (p->right->type==2 &&GetRank(p->right->data)<=GetRank(p->data)) { str[strlen (str)]='(' ; strcat (str,p->right->code); str[strlen (str)]=')' ; str[strlen (str)]=0 ; } else strcat (str,p->right->code); } else sprintf (str,"%.0f" ,p->data); } } int main () { DataType Num=0 ;int Flag=0 ,op; char s[200 ]; gets(s);scanf ("%d" ,&op); for (int i=0 ;s[i]&&s[i]!='\n' ;i++) { if (s[i]>='0' &&s[i]<='9' ) { Num=(DataType)(Num*10 +s[i]-'0' ); Flag=1 ; } else if (s[i]==' ' ) { if (Flag) { InStack(Num,1 ); Flag=0 ;Num=0 ; } } else InStack((DataType)s[i],2 ); } TreePtr root=StackTree[--TopTree]; DFS(root); if (op==2 ) printf ("%s\n" ,root->code); printf ("%.2f" ,root->num); return 0 ; }
网络打印机选择
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct tree { int Id,type; struct tree *next [8],*Far ; }; typedef struct tree *TreePtr ;typedef struct tree Tree ;TreePtr PosId[400 ]; void InTree (int Id,int FarId,int type,int pos) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); memset (q->next,0 ,sizeof (q->next)); q->Id=Id;q->type=type; if (Id) { TreePtr FarPtr=PosId[FarId]; FarPtr->next[pos]=q; q->Far=FarPtr; } PosId[Id]=q; } int Map[100 ],map [100 ],min=400 ,tar;int visited[400 ]={0 };void DFS (TreePtr p,int now) { if (p!=NULL ) { if (!visited[p->Id]) { visited[p->Id]=1 ; map [now]=p->Id; if (p->type==2 &&now<min) { for (int i=0 ;i<now;i++) Map[i]=map [i]; min=now;tar=p->Id; } if (p->type==0 ) for (int i=0 ;i<8 ;i++) DFS(p->next[i],now+1 ); if (p->Far!=NULL ) DFS(p->Far,now+1 ); } } } int main () { FILE *open=fopen("in.txt" ,"r" ); int Id,FarId,type,pos; int n,m; while (~fscanf (open,"%d%d%d%d" ,&Id,&FarId,&type,&pos)) InTree(Id,FarId,type,pos); scanf ("%d%d" ,&n,&m); TreePtr root=PosId[m]; DFS(root,0 ); printf ("%d " ,tar); for (int i=1 ;i<min;i++) printf ("%d " ,Map[i]); return 0 ; }
2019
空闲空间合并
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct node { int left,right; } space[200 ]; int cmp (const void *e1,const void *e2) { struct node *p =struct node*)e1; struct node *q =struct node*)e2; if (p->left==q->left) return (p->right<q->right)?-1 :1 ; else return (p->left<q->left)?-1 :1 ; } int main () { int n,left,right; scanf ("%d" ,&n); for (int i=0 ;i<n;i++) scanf ("%d%d" ,&space[i].left,&space[i].right); qsort(space,n,sizeof (space[0 ]),cmp); for (int i=0 ;i<n-1 ;i++) { int num=space[i].right; for (int j=i+1 ;j<n;j++) { if (space[j].left==num+1 ) { num=space[j].right; space[j].left=100010 ; } } space[i].right=num; } qsort(space,n,sizeof (space[0 ]),cmp); for (int i=0 ;i<n;i++) { if (space[i].left!=100010 ) printf ("%d %d\n" ,space[i].left,space[i].right); } return 0 ; }
火车货运调度模拟
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct PosNode { char name[100 ]; int distance; }PosID[60 ]; typedef struct trainNode {int id,distance;} Node,*NodePtr;NodePtr stackB[100 ],stackA[100 ]; int topA=0 ,topB=0 ;int n,m,sum=0 ;int SearchDistance (char name[]) { for (int i=0 ;i<n;i++) if (strcmp (name,PosID[i].name)==0 ) return PosID[i].distance; return 0 ; } int main () { freopen("a.in" ,"r" ,stdin ); freopen("a.out" ,"w" ,stdout ); int id; char name[100 ]; scanf ("%d" ,&n); for (int i=0 ;i<n;i++) scanf ("%s %d\n" ,PosID[i].name,&(PosID[i].distance)); scanf ("%d" ,&m);topB=m-1 ; for (int i=0 ;i<m;i++) { scanf ("%d %s\n" ,&id,name); NodePtr q=(NodePtr)malloc (sizeof (Node)); q->id=id;q->distance=SearchDistance(name); stackB[topB--]=q; } topB=m; while (topB) { int max=0 ,pos=topB; for (int i=topB-1 ;i>=0 ;i--) { if ((stackB[i])->distance>max) { max=(stackB[i])->distance; pos=i; } } stackA[topA++]=stackB[pos]; if (pos==topB-1 ) sum++; else { sum+=topB-pos+1 ; for (int i=pos;i<topB-1 ;i++) stackB[i]=stackB[i+1 ]; } topB--; } for (int i=0 ;i<topA;i++) printf ("%04d " ,(stackA[i])->id); printf ("\n%d" ,sum); return 0 ; }
查找同名文件
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct tree { char name[100 ]; int time,type; struct tree *next [110]; }; typedef struct tree *TreePtr ;typedef struct tree Tree ;TreePtr root=NULL ; TreePtr PosId[300 ]; int now=0 ;TreePtr GetPos (char name[]) { for (int i=0 ;i<now;i++) if (strcmp (name,(PosId[i])->name)==0 ) return PosId[i]; return NULL ; } void InTree (char name[],char nameFar[],int type,int time) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); memset (q,0 ,sizeof (Tree)); strcpy (q->name,name);q->type=type;q->time=time; PosId[now++]=q; if (strcmp (nameFar,"-" )==0 ) root=q; else { TreePtr far=GetPos(nameFar); for (int i=0 ;i<110 ;i++) { if (far->next[i]==NULL ) { far->next[i]=q; break ; } } } } struct node { char str[200 ]; int time,pos; struct node *link ; }; typedef struct node *NodePtr ;typedef struct node Node ;NodePtr head=NULL ; void InNode (char str[],int time,int pos) { NodePtr q=(NodePtr)malloc (sizeof (Node)); strcpy (q->str,str);q->link=NULL ; q->time=time;q->pos=pos; if (head==NULL ) head=q; else if ((time>head->time)||(time==head->time&&pos<head->pos)) { q->link=head; head=q; } else { NodePtr p=head,r=NULL ; for (;p!=NULL ;r=p,p=p->link) { if ((time>p->time)||(time==p->time&&pos<p->pos)) { r->link=q; q->link=p; break ; } } if (p==NULL ) r->link=q; } } TreePtr map [100 ]; void DFS (TreePtr p,char name[],int pos) { if (p!=NULL ) { map [pos]=p; if (strcmp (p->name,name)==0 ) { char str[200 ]={0 }; for (int i=0 ;i<pos;i++) { strcat (str,(map [i])->name); str[strlen (str)]='\\' ; str[strlen (str)]=0 ; } strcat (str,name); str[strlen (str)]=0 ; InNode(str,p->time,pos); } for (int i=0 ;i<110 ;i++) DFS(p->next[i],name,pos+1 ); } } int main () { char name[100 ],nameFar[100 ]; int time,type,count; FILE *open=fopen("files.txt" ,"r" ); while (~fscanf (open,"%s %s %d %d\n" ,name,nameFar,&type,&time)) InTree(name,nameFar,type,time); scanf ("%d %s\n" ,&count,name); DFS(root,name,0 ); for (NodePtr p=head;p!=NULL ;p=p->link) printf ("%s\n" ,p->str); return 0 ; }
2020
机试异常检测(简)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct info { int id,pos,time; char name[100 ]; } stu[300 ]; int now=0 ;int GetPos (int id) { for (int i=0 ;i<now;i++) if (stu[i].id==id) return i; return -1 ; } int cmp (const void *e1,const void *e2) { int a=*(int *)e1; int b=*(int *)e2; if (stu[a].id==stu[b].id) return 0 ; else return (stu[a].id<stu[b].id)?-1 :1 ; } int main () { int n,id,pos,time; int error[100 ]={0 },cnt=0 ; char name[100 ]; scanf ("%d" ,&n); for (int i=0 ;i<n;i++) { scanf ("%d %s %d %d\n" ,&id,name,&pos,&time); int num=GetPos(id); if (num==-1 ) { stu[now].id=id; stu[now].time=time; stu[now].pos=pos; strcpy (stu[now].name,name); now++; } else { if (pos!=stu[num].pos) { int j; for (j=0 ;j<cnt;j++) if (error[j]==num) break ; if (j==cnt) error[cnt++]=num; } } } qsort(error,cnt,sizeof (error[0 ]),cmp); for (int i=0 ;i<cnt;i++) printf ("%d %s\n" ,stu[error[i]].id,stu[error[i]].name); return 0 ; }
函数调用关系
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct node { char name[100 ]; int cnt,SonId[100 ]; } fun[100 ]; int now=0 ;int GetId (char name[]) { for (int i=0 ;i<now;i++) if (strcmp (fun[i].name,name)==0 ) return i; return -1 ; } int stack [100 ],top=0 ;void InStack (char name[]) { int id=GetId(name); if (id==-1 ) {id=now;strcpy (fun[now++].name,name);} if (top) { int far=stack [top-1 ],i; int *tar=fun[far].SonId; for (i=0 ;i<fun[far].cnt;i++) if (tar[i]==id) break ; if (i==fun[far].cnt) { tar[i]=id; fun[far].cnt++; } } stack [top++]=id; } int main () { int op; char name[100 ]; memset (fun,0 ,sizeof (fun)); scanf ("%d %s\n" ,&op,name); InStack(name); while (top) { scanf ("%d" ,&op); if (op==0 ) top--; else { scanf ("%s\n" ,name); InStack(name); } } for (int i=0 ;i<now;i++) { if (fun[i].cnt) { printf ("%s:" ,fun[i].name); for (int j=0 ;j<fun[i].cnt;j++) printf ((j==fun[i].cnt-1 )?"%s\n" :"%s," ,fun[(fun[i].SonId)[j]].name); } } return 0 ; }
服务优化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct tree { int id; struct tree *next [3]; }; typedef struct tree *TreePtr ;typedef struct tree Tree ;struct node {int id,num;} data[200 ];int now=0 ;TreePtr PosId[1000 ]; TreePtr line[2000 ]; int head=0 ,rear=0 ;int cmp (const void *e1,const void *e2) { struct node *p =struct node *)e1; struct node *q =struct node *)e2; if (p->num==q->num) return (p->id<q->id)?-1 :1 ; else return (p->num<q->num)?1 :-1 ; } int main () { int id,num,far; TreePtr r=(TreePtr)malloc (sizeof (Tree)); memset (r,0 ,sizeof (Tree));r->id=100 ; PosId[100 ]=r; scanf ("%d" ,&far); while (~far) { TreePtr FarTree=PosId[far]; scanf ("%d" ,&id); while (~id) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); memset (q,0 ,sizeof (Tree));q->id=id; PosId[id]=q; for (int i=0 ;i<3 ;i++) if (FarTree->next[i]==NULL ) {FarTree->next[i]=q;break ;} scanf ("%d" ,&id); } scanf ("%d" ,&far); } while (~scanf ("%d %d" ,&id,&num)) { data[now].id=id; data[now].num=num; now++; } qsort(data,now,sizeof (data[0 ]),cmp); TreePtr root=PosId[100 ]; line[0 ]=root;now=0 ; while (head<=rear) { TreePtr p=line[head++]; if (p->id<100 ) printf ("%d->%d\n" ,data[now++].id,p->id); for (int i=0 ;i<3 ;i++) if (p->next[i]!=NULL ) line[++rear]=p->next[i]; } return 0 ; }
2021
汉明距离
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct sen { char word[200 ]; int diff; } str[200 ]; int cmp (const void *e1,const void *e2) { struct sen * p =struct sen *)e1; struct sen * q =struct sen *)e2; if (p->diff==q->diff) return strcmp (p->word,q->word); else return (p->diff<q->diff)?-1 :1 ; } int main () { int n;char s[200 ]={0 }; scanf ("%d\n%s\n" ,&n,s); memset (str,0 ,sizeof (str)); for (int i=0 ;i<n-1 ;i++) { scanf ("%s\n" ,str[i].word); for (int j=0 ;j<200 ;j++) if ((str[i].word)[j]!=s[j]) str[i].diff++; } qsort(str,n-1 ,sizeof (str[0 ]),cmp); for (int i=0 ;i<n-1 ;i++) printf ("%s %s %d\n" ,s,str[i].word,str[i].diff); return 0 ; }
二叉搜索树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> struct tree { int data,count; struct tree *left ,*right ; }; typedef struct tree *TreePtr ;typedef struct tree Tree ;TreePtr root=NULL ; int sum=0 ;void InTree (int data) { TreePtr q=(TreePtr)malloc (sizeof (Tree)); q->data=data;q->count=1 ; q->left=q->right=NULL ; if (root==NULL ) root=q; else { TreePtr p=root; while (1 ) { sum++; if (data==p->data) {p->count++;break ;} else if (data>p->data) { if (p->right==NULL ) {p->right=q;break ;} else p=p->right; } else if (data<p->data) { if (p->left==NULL ) {p->left=q;break ;} else p=p->left; } } } } int Map[20 ]={0 },map [20 ]={0 },max=0 ;void DFS (TreePtr p,int now) { if (p!=NULL ) { map [now]=p->data; if (p->count>max) { for (int i=0 ;i<=now;i++) Map[i]=map [i]; Map[now+1 ]=0 ; max=p->count; } DFS(p->left,now+1 ); DFS(p->right,now+1 ); } } int main () { int n,num; scanf ("%d" ,&n); for (int i=0 ;i<n;i++) { scanf ("%d" ,&num); InTree(num); } printf ("%d\n" ,sum); DFS(root,0 ); for (int i=0 ;Map[i]!=0 ;i++) printf ("%d " ,Map[i]); return 0 ; }
解释系统
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 #include <stdio.h> #include <ctype.h> #include <string.h> #include <math.h> #include <stdlib.h> typedef double DataType;#define RankTop 100 DataType StackNum[1000 ]; char StackOp[1000 ];int TopNum=0 ,TopOp=0 ;struct NameId { char name[100 ]; DataType data; } Board[1000 ]; int count=0 ;int GetId (char name[]) { for (int i=0 ;i<count;i++) if (strcmp (name,Board[i].name)==0 ) return i; strcpy (Board[count].name,name); Board[count++].data=0 ; return count-1 ; } int GetRank (char op) { int rank; switch (op) { case '+' :case '-' :rank=1 ;break ; case '*' :case '/' :rank=2 ;break ; case '(' :rank=RankTop;break ; } return rank; } void Compute (char op) { DataType Right=StackNum[--TopNum]; DataType Left=StackNum[--TopNum]; DataType Now; switch (op) { case '+' :Now=Left+Right;break ; case '-' :Now=Left+Right;break ; case '*' :Now=(DataType)(Left*Right);break ; case '/' :Now=(DataType)(Left/Right);break ; } StackNum[TopNum++]=Now; } void OpPut (char op) { if (TopOp==0 ) StackOp[TopOp++]=op; else if (op==')' ) { while (TopOp&&StackOp[TopOp-1 ]!='(' ) Compute(StackOp[--TopOp]); if (TopOp&&StackOp[TopOp-1 ]=='(' ) TopOp--; } else { while (TopOp&&StackOp[TopOp-1 ]!='(' &&GetRank(StackOp[TopOp-1 ])>=GetRank(op)) Compute(StackOp[--TopOp]); StackOp[TopOp++]=op; } } DataType GetNum (char s[]) { char name[100 ]; int Flag=0 ,now=0 ; DataType Num=0 ; for (int i=0 ;s[i]&&s[i]!='\n' ;i++) { if (s[i]==' ' ) continue ; else if (s[i]>='0' &&s[i]<='9' ) { Num=Num*10 +s[i]-'0' ; Flag=1 ; } else if (s[i]>='a' &&s[i]<='z' ) { name[now++]=s[i]; Flag=1 ; } else { if (Flag) { name[now]=0 ; if (now) Num=Board[GetId(name)].data; StackNum[TopNum++]=Num; Num=0 ;now=Flag=0 ; } OpPut(s[i]); } } if (Flag) { name[now]=0 ; if (now) Num=Board[GetId(name)].data; StackNum[TopNum++]=Num; } while (TopOp) Compute(StackOp[--TopOp]); return StackNum[--TopNum]; } int main () { char Exit[]="exit" ,Print[]="print" ; char str[1000 ],name[100 ]; int now=0 ; gets(str); while (strcmp (str,Exit)) { char *p=strstr (str,Print); if (p!=NULL ) { for (int i=(int )(p-str)+6 ;str[i]&&str[i]!='\n' ;i++) { if (str[i]==' ' ) { if (now) { name[now]=0 ;now=0 ; printf ("%.2f " ,Board[GetId(name)].data); } } else name[now++]=str[i]; } if (now) { name[now]=0 ;now=0 ; printf ("%.2f " ,Board[GetId(name)].data); } printf ("\n" ); } else { int i=0 ; for (;str[i]!='=' ;now++,i++) name[now]=str[i]; name[now]=0 ;now=0 ; Board[GetId(name)].data=GetNum(str+i+1 ); TopNum=TopOp=0 ; } gets(str); } return 0 ; }



 能处理负权值的情况(不能得到最远距离)
能处理负权值的情况(不能得到最远距离)




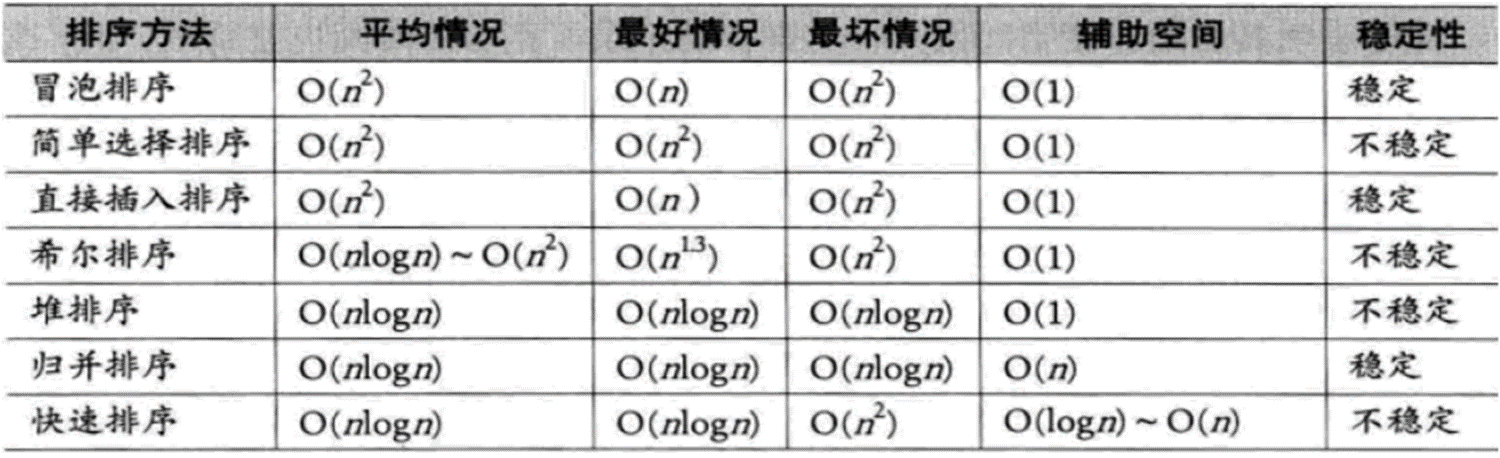 从算法性质来看:
从算法性质来看:
