物理学家总是热衷于寻找不变量。在惯常思考的经典物理学世界中,长度是不变的,其表达式为:Δl=Δx2+Δy2+Δz2,在不同的参考系中,如直角坐标系、极坐标系、柱坐标系中,总能够都是一样的结果。
线元确定几何,每当确定了线元时,总可以确定其他的各种变量,故此时我们需要找到一个不变的,具有线元量纲的量。
那么在相对论的世界中呢,我们直到洛伦兹变换:
⎩⎨⎧x′=1−c2v2x−vty′=yz′=zt′=1−c2v2t−c2xv
此时如果再计算Δl,会发现在相对论情境下,其并不是一个守恒量。
这时候,对于
ΔS′2=Δx′2+Δy′2+Δz′2−(c∗Δt′)2=(1−c2v2Δx−vΔt)2+Δy2+Δz2−(v∗1−c2v2Δt−c2Δxv)2=Δx2+Δy2+Δz2−(c∗t)2=ΔS2
故在相对论情况下,记ΔS=Δx2+Δy2+Δz2−(cΔt)2为洛伦兹不变量,在闵氏几何的任意参考系中不变。
通常也会通过单位化记c=1,使得此时ΔS=Δx2+Δy2+Δz2−Δt2
世界线
时空图
世界线:在闵氏几何中,有四个坐标x,y,z,t,可以代表物体所有的时空信息,故一个粒子在任意时刻的时空信息就是时空图上的一个点,连成一条线成为世界线。
为了进行简化(发不出思维),通常只保留x,t坐标进行绘制时空图。

同时的相对性
对于火车问题:在地系中,闪电同时击中车位,在车中,人看到的并不同时,即为:同时的相对性
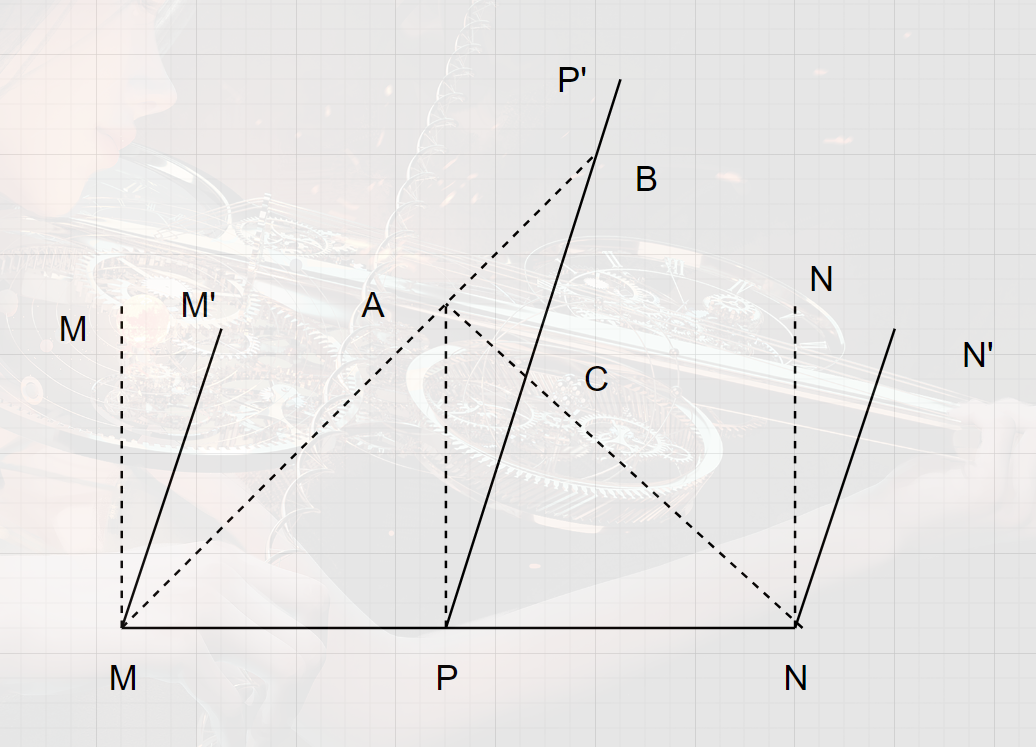

其中,M’,P’,N’为运动火车上的点
洛伦兹变换的时空观图体现
对于洛伦兹变换:
⎩⎨⎧x′=1−c2v2x−vt=γ(x−vt)y′=yz′=zt′=1−c2v2t−c2vx=γ(t−vx)
对于x′,找到t′=0的对应于xt=v,对于t′对应于xv=v1,即对应x′轴和t′轴
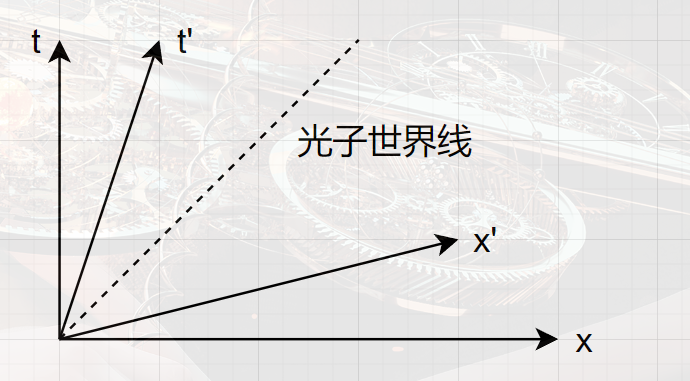
闵氏几何中的线长
在欧式几何中,l2=Δx2+Δy2,在闵氏几何中,l2=∣Δx2−Δt2∣。
对于如图所示的尺子世界面,在S系中测量长度为OA,在S′系中国为OD,但是由闵氏几何的计算规则,显然有OD<OA,者就是尺缩效应。(静止系中测量运动物体长度)
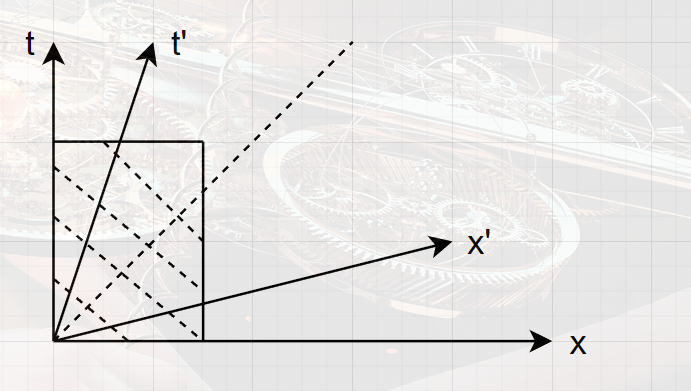
世界线长度等于固有时
对于任意物体的任意参考系,在其本征系中,Δx始终为0,故在其本征系中,世界线长度等于固有时,由于每个惯性系中世界线长度一样长,故在任何惯性系中,世界线的长度都等于固有时。
在相对论时空中:
ds2=(cdt)2−(dl)2=(cdt)2
记固有时dτ=cds。
对于AB,显然l1>l2,故有l1的运动方式所经过的固有时大于l2的方式:双生子佯谬。
其中l1为静止,l2有速度。
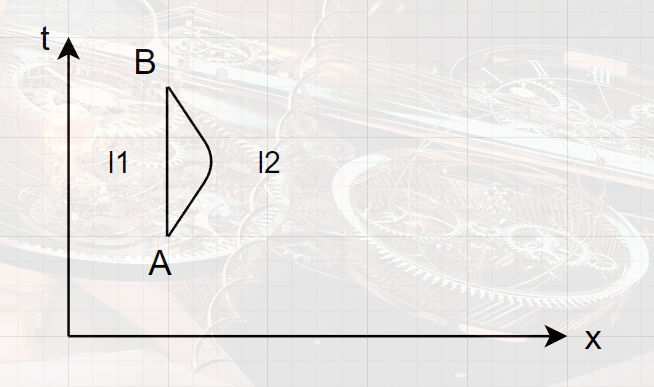
讨论:相对性
依照相对运动的观点,哥哥高速远离地球,按照这么来说哥哥所经历的固有时短,这没问题,但是从相对运动的角度来讲,难道不应该有弟弟相对哥哥告诉原理,在相对哥哥静止的参考系中,弟弟所经历的固有时短,相遇时这不矛盾了吗。
问题的核心在于:惯性运动和非惯性运动的区别是绝对的,哥哥必然有一个加速-减速的过程,和弟弟呆在地球上近似惯性的运动是不同的。无论从哪个惯性系出发,哥哥弟弟两人的世界线长度不变,但是若换到哥哥的系中,是一个非惯性系,不符合狭义相对论要求的惯性参考系条件,不能够从固有时的角度进行思考。
所以要从一个惯性参考系角度进行分析,分别和相遇都是相对地球系,也就是弟弟系,认为近似于一个惯性参考系,所以才可以从固有时角度进行分析。
四维矢量
利用w=ict对洛伦兹变换进行改写:
⎩⎨⎧x′=γ(x+iβw)y′=yz′=zw′=γ(w−iβx)
定义:如果A=(Ax,Ay,Az,At)与(x,y,z,w)一样符合洛伦兹变换,则称为四维矢量:
⎩⎨⎧Ax′=γ(Ax+iβAt)Ay′=AyAz′=AzAt′=γ(At−iβAx)
其中A2=Ax2+Ay2+Az2+At2成为洛伦兹变换下的不变量。
对于两个四维矢量A,B,其点积A∗B=AxBx+AyBy+AzBz+AtBt,也是洛伦兹变换下的不变量。
证明:
A′∗B′=Ax′Bx′+Ay′By′+Az′Bz′+At′Bt′=γ2(Ax+iβAt)(Bx+iβBt)+γ2(At−iβAx)(Bt−iβBx)+Ay′By′+Az′Bz′=γ2(1−β2)(AxBx+AtBt)+Ay′By′+Az′Bz′=AxBx+AyBy+AzBz+AtBt=A∗B
四维速度
对于固有时dτ,在本征系中,时空间隔ds2=(cdτ)2−(dl)2=(Cdτ)2,故dτ=cds。
定义四维速度:
⎩⎨⎧ux=dτdxuy=dτdyuz=dτdzux=dτdw
故由dτdt=1−c2v2vx,可得
ux=dtdx∗dτdt=vx∗dτdt=1−c2v2vx,uy=1−c2v2vy,uz=1−c2v2vz,ut=dtdw∗dτdt=1−c2v2ic
其中dτ对应的时间为本征系S′,u对应S系而不是本征系S’。
故有四维速度:
u=(ux,uy,uz,ut)=(γvx,γvy,γvz,γic)
且u2=ux2+uy2+uz2+ut2=−c2。
四维速度符合洛伦兹变换
在S系中,物体以v=(vx,vy,vz)运动,S′系相对S系以V运动,则四维速度u′有
⎩⎨⎧ux′=γV(ux+iβVut)uy′=uyuz′=uzut′=γV(ut−iβVux)
故可得:
⎩⎨⎧ux′=γ′vx′=γV(γ∗vx+iβV∗8cγ)=γ∗γV(vx−cβV)①uy′=γ′vy′=γvy②uz′=γ′vz′=γvz③ut′=icγ′=γV(icγ−iβV−γvx)=iγγV(c−βVvx)④
由④可得:
γ′γV−γ=1−c2V∗vx1
带入①②③,可得:
vx′=1−c2V∗vxvx−Vvy′=γV(1−c2V∗vx)vyvz’=γV(1−c2V∗vx)vz
四维动量
对于一般动量P=γmv,其中γv是四维速度的前三个分量,故可以定义四维动量:
p=m0u=m0(γvx,γvy,γvz,iγc)
其中第四个分量为pt=m0iγc=icE.
四维动量的模方为:
p2=px2+py2+pz2+pt2=P2−c2E2=−m02c2
为一个不变量。
四维动量符合洛伦兹变换
由于四维动量的前三项均为速度分量,最后一项与E相关,故可将运动方程中的两个基本方程:
{P1+P2+P3+...=P1′+P2′+P3′+...E1+E2+E3+...=E1′+E2′+E3′+...
整合为四维动量守恒方程:
p1+p2+p3+...=p1′+p2′+p3′+...
根据模方等进行计算。
例:利用四维动量推到光的洛伦兹变换
能量E=hν,动量P=λh=cE
由于p符合洛伦兹变换,故E也符合洛伦兹变换,故有:E=γ(E′−βcPx′),
其中
Px′=P′∗cosθ=cE′cosθ′
故有:
ν=γν′(1−βcosθ′)=ν′1−β21−βcosθ′
则:
νν′=1−βcosθ′1−β2
当β<<1且θ=2π时,有νν′=1−β2=1−21β2,说明横向多普勒红移是β2级的微弱效应,在经典情境中为0.
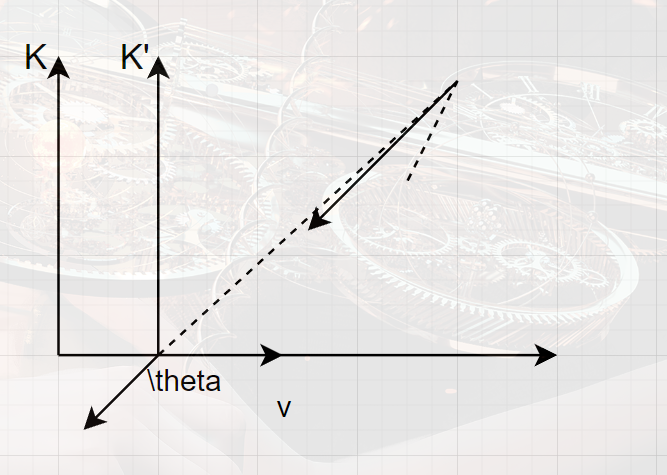
角分布的变化
在本节的讨论中,以粒子的动量分布作为粒子分布的代表,在理想的实验情境中,应为均匀分布(在P=∣P∣相等的条件下)。
在相对论条件下,在质心系中,粒子依然均匀分布,但在实验室系中,由洛伦兹变换:
⎩⎨⎧Px′=γ(Px+iβcE)Py′=PyPz′=PzE′=γ(E−iβpc2)
在实验室系中,原来的球被拉伸为一个椭球,中心平移到Px′=γβcE=γmVc处,半长轴为γp=γmv,半短轴为p=mv。其中v为在质心系中各向同性的速率。
-
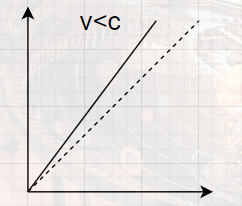
v<Vc
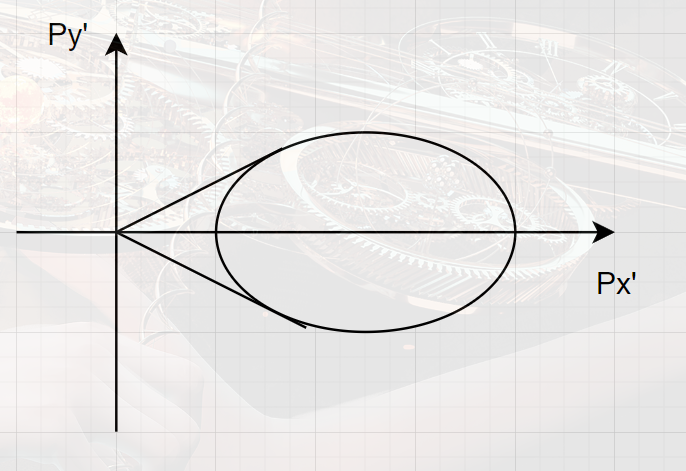
-
v>Vc

-
v=Vc
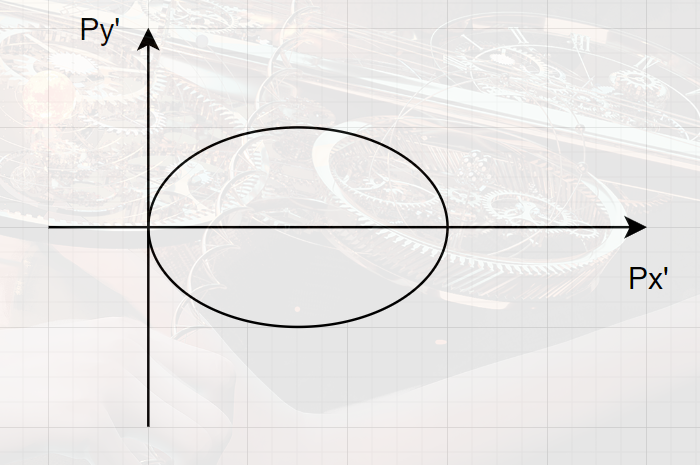
无论如何,总是被拉长代的,半顶角θ0满足:
θ0≈γβcEp=γβ1≈γ1=1−β2→0,β→1
像一个探照灯,具有高度的定向性。
电磁变换
狭义相对论:任何物理规律在惯性系中相同。
参考系变换后电荷的运动状态改变,但是受力不变:电磁具有高度的统一性,在不同参考系中相互转换。
参考文献











