面向对象-Unit1-递归下降

递归下降

d文法

文法是对语言结构的定义和描述，也就是通过形式化的表述来规定语言结构的规则。

文法，是语言的规则。文法讨论的范围较宽，此处仅关注词法和语法。

词法

词法是指语言中的词汇及其属性和含义的规则。它规定了一个语言中的"词"是如何构成的。

例如有一个语法单元：变量名，定义其为由大于0个小写字母组成的字符串,那么就可以写成

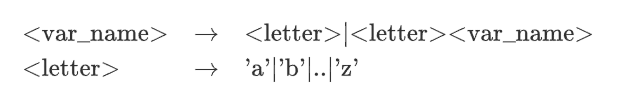
1. 尖括号内表示一个语法成分
2. 右箭头表示左侧的部分由右侧的部分组成
3. 竖线 “|” 表示可以选择右边的规则可以选取竖线两侧的任一种情况。
   1. 这种表示方式赋予了词法的递归性质，即可以不断定义更长的词法

由此就可以得到变量名的构成规则。

语法

语法是指描述语言中句子结构和组织方式的规则。它规定了一个语言中的"句"是如何构成的。

例如下面的例子：

通过这个规则我们知道,句子是一个主语加上一个谓语连在一起构成的。其中主语可能是i也可能是you，谓语可能是smile，可能是laugh。

字符串解析

程序做的绝大多数事情都是在解析字符串，有了词法和语法后，有了解析的规则。那么，该如何使用合适的结构和方法来降低复杂性呢？

Token

有了词法和语法的定义后，自然地想要对字符串进行解析。

一个自然的思路是：

1. 认为字符串是一个句，按照语法规则将句拆分为词
2. 按照词法规则再对词进行字符解析

在计算机领域，token常常用来表示文本的最小语法单位。可以以token来存储字符串经过词法分析得到的一个个单元。不妨假设用一个list来存储分析得到的token，那么每识别出一个token，就可以向这个列表中加上它。这样，经过一遍扫描，我们就可以将一个字符串的信息整合转化成一个token的列表。

//str: iloveyou
for(int i=0;i<str.size();i++){
  if(str.charAt(i)=='i'){
    tokenList.add(new Token("i","主语"));
  }
  else if(str.charAt(i)=='y'){
    i=i+2;
    tokenList.add(new Token("you","主语"));
  }
  else if(str.charAt(i)=='s'){
    i=i+4;
    tokenList.add(new Token("smile","谓语"));
  }
  else{
    i=i+4;
    tokenList.add(new Token("laugh","谓语"));
  }
}

语法分析

利用词法规则可以将字符串转换为由token组成的token列表，可以进行下一步的语法分析

从代码设计的角度上来看，通过将字符串经过词法分析转化为 “token” 列表，词法分析这一道工序将半成品tokenList传入到下一道工序：语法分析，而不是直接在语法分析阶段调用词法的解析，能够很好的减少这两个不同级别处理之间的耦合。

为了说明如何进行语法分析，这里引入一个规则，该规则阐释了一个表达式的语法结构：

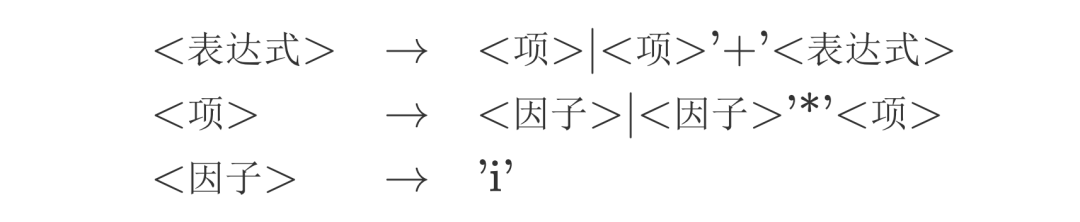
事实上，我们可以很容易看出，在这个结构中：

• 表达式 = 项+项…+项
• 项 = 因子*因子*因子
• 因子用一个字母i表示，不可再分。

最外层是表达式，表达式可以被看作是几个项的和，项可以被看作是几个因子的乘积。一个表达式的结构很明显的分成了三层。

表达式层次分析

表达式的“三层”，用图像来表示的话应当是下面的样子。

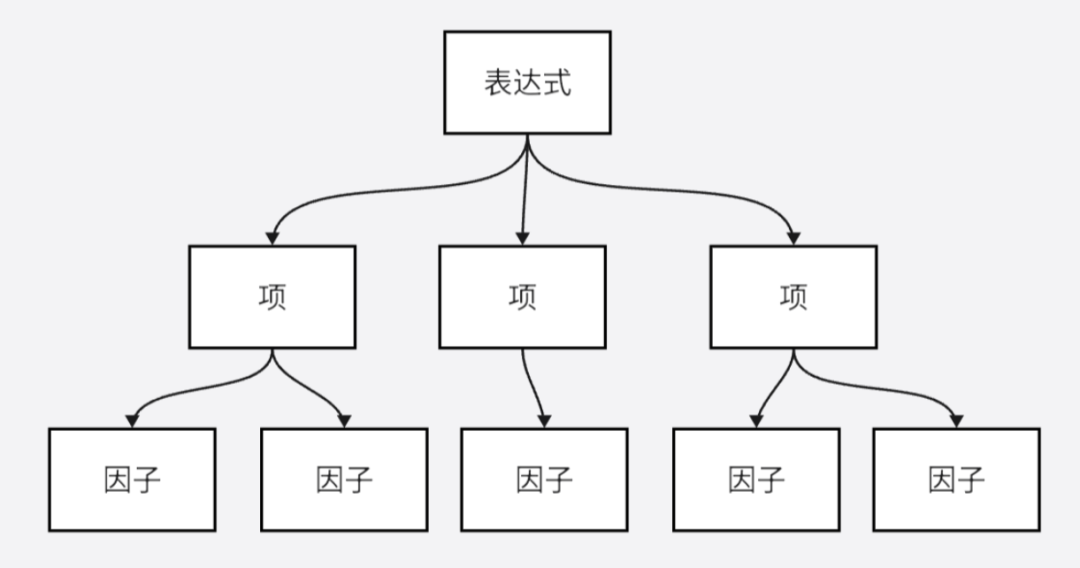
语法分析的目的就是生成一个这样的树，它用节点之间的联系来表达原本表达式的语法结构。这种树一般被称为语法树（Syntax Tree）或抽象语法树（Abstract Syntax Tree，AST）

可以用类来构建一下这个语法树的几个节点类,其中表达式用Expr表示，项用Term表示，因子用Factor表示：

public class Expr{
  private ArrayList<Term>terms;
}

public class Term{
  private ArrayList<Factor>factors;
}

public class Factor{
}

下降

如果从全局的视角来看，综合考虑所有的规则，就会得到上面图中的语法树。它的大小，宽度和深度随着规则的扩张而不断增加，规则条数越多，树越复杂，要从全局的视角来处理也就越困难，可以想象一下添加若干将因子再拆成更低层的组成部分的情况：

那么从全局来看，语法树将会变得十分的庞大和复杂，解析它的程序也会变得复杂起来。

但是实际上，一个节点有关的语法结构，是不随其所在的位置变化的：某个Term无论是Expr的第几个Term，它的构成规则也不会改变，都是由若干个因子和若干个"*"按次序排布构成。这个局部的性质，不随其在全局的位置和周围的状态改变。所以，不妨把全局的视角，"短视地"移动到局部，那么就能从语法树中提取出这样的的一个结构：

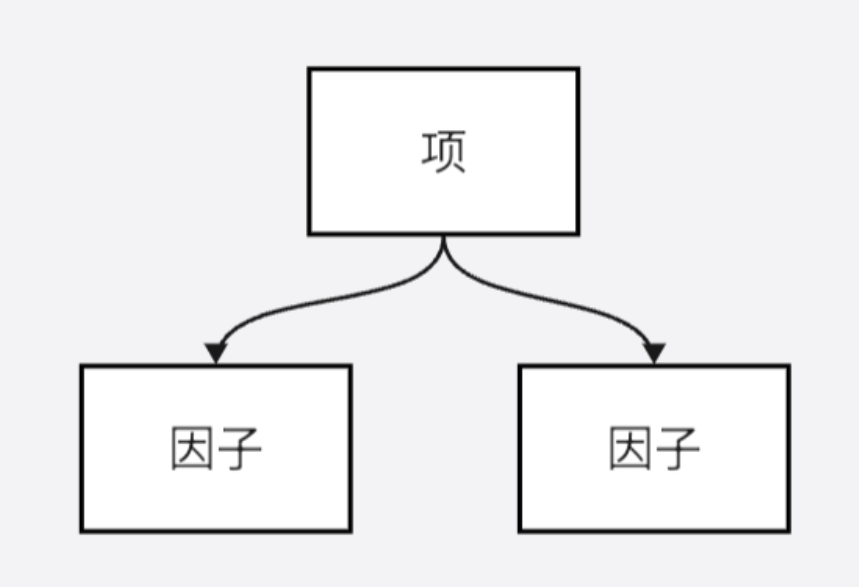
这个结构揭示了这样一个事实：不用管项从哪里来，只需要知道项往哪里去，就能够处理好项的解析。如果仅仅将这一部分的逻辑抽象出来写一段程序，想必比之前写整个树的程序轻松不少。再往上的另一条规则，也可以被单独抽象出来：

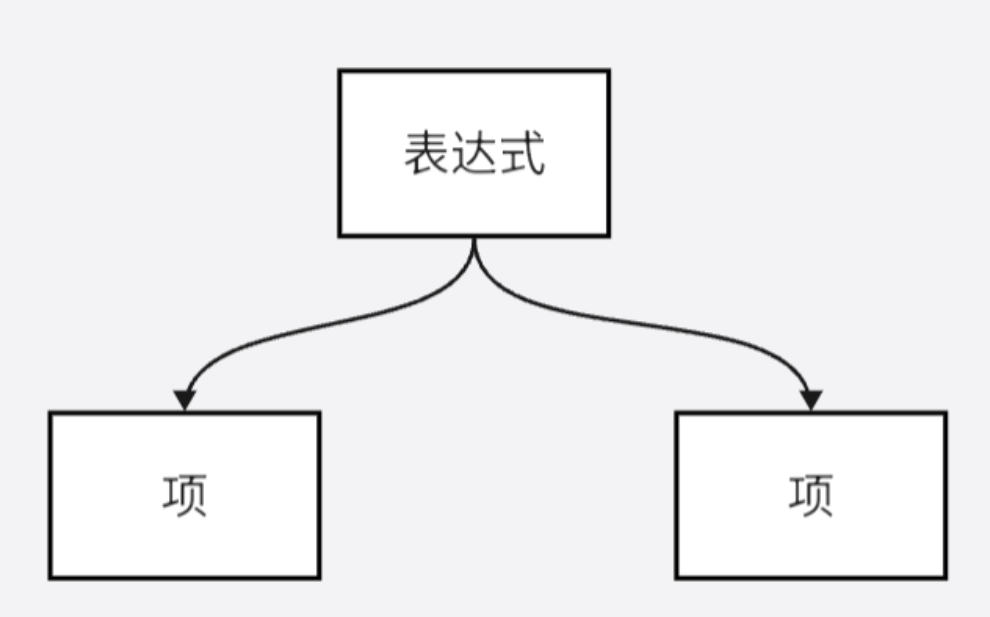
一个表达式，就是几个项而已。如果我们能够在这里屏蔽项的解析过程，而直接返回项的解析结果，那么就可以将表达式的解析过程化简为一次简单的下降。

这个观点非常重要，请同学们细细品味。可能在以往的代码编写中，同学们习惯将解决一个局部问题的具体过程嵌入到更高层次代码的编写中(例如在这俩将解析项的具体过程直接写到解析表达式的过程中)。

但事实上，让逻辑变简单的一个方法是，在高层次的代码编写中忽视局部问题的解决过程，假设其已经被某个方法解决，从而直接调用该方法即可。

选择合适的局部视角，合理的屏蔽细节，将具体的实现封装，是让代码高效且清晰的重要手段。

这样的逻辑实际上就是封装，使用不同层次的处理方法，上层不用关注下层的处理规则，认为下层能够返回相应的结果。

可以给出相应的伪代码示意：

1. 对表达式的处理parserExpr

   parserExpr:
     新建一个Term的容器T
     调用parserTerm获得一个项t
     T中加上parserTerm返回的项t
     while 当前token是+:
       跳过当前token(+)
       调用parserTerm获得一个项t
       T中加上parserTerm返回的项t
     利用T生成一个新的Expr e
     返回e

2. 对项的处理parserTerm

   parserTerm:
     新建一个Factor的容器F
     调用parserFactor获得一个因子f
     F中加上parserFactor返回的因子f
     while 当前token是*:
       跳过当前token(*)
       调用parserFactor获得一个因子f
       F中加上parserFactor返回的因子f
     利用F生成一个新的Term t
     返回t

3. 对因子的处理parserFactor

   parserFactor:
     检查当前的token是否是i
     跳过当前的token(i)
     利用i生成一个新的Factor f
     返回f

递归

必须指出的是，如果我们不曾听说过或者学习过类似的观点，也可以用一个多层的循环来简单地解决这个问题。这是因为我们上面题面给出的语法结构所形成的树，具有固定的层数，我们可以清楚的知道这个树的终结就在子节点的factor 处。

为了更好地说明递归下降法地意义，可以修改一下上述因子的语法规则：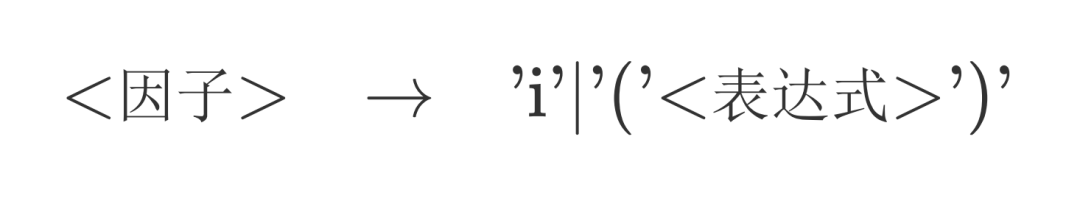

这么做的话，语法树就不是简单的三层了。甚至并不知道它的层数，因为任何一个因子都可以通过解析为表达式的方式来不断的向下扩张，这无疑给了我们很大的复杂性。我们的解析流程，可能会呈现：**<表达式>-<项>-<因子>-<表达式>**的递归调用过程。如果再从全局的视角来看，这个语法树的宽度和深度等性质不再可知，它已经变得不可捉摸了。

但是我们从局部的视角来看，会发现表达式的语法规则没有变，项的也没有变，唯一变的是因子，所以我们只需要修改上面的parseFactor过程就好。

parserFactor:
  检查当前的token是否是i
  if 真:
    跳过当前的token(i)
    利用i生成一个新的Factor f
    返回f
  if 假，说明是(表达式):
    跳过当前token(()
    调用parserExpr()获得一个表达式e
    利用e生成因子f
    跳过当前token())
    返回f

具体的递归下降

这里我们需要总结一下：

1. 递归下降分析方法的主要做法是，对文法每条规则的左部符号（ ‘→’ 左侧的符号），建立一个解析子程序，用以完成该符号所代表成分的分析和识别。
2. 对于每个符号的分析子程序的功能则是，用该符号对应文法中的规则来匹配输入的token流。

根据我们上面的例子可以看到，递归下降算法的思想严格依照文法来编写，甚至可以理解为文法的一种“翻译”，递归下降正是依托于文法保证了该算法的正确性。

递归下降分析法作为自顶向下的分析过程，其一级一级的向下分配任务，通过检测当前符号和预期符号 （文法中的规则） 的相符性来选择"分支"进行解析，进而建立结构。

对于上述表达式规则，做法通常为：

1. 建类

   在→左面的部分都是我们需要进行分析的语法成分，因此需要对其进行建类，并且构造解析方法。

   1. 表达式类 → Expr
   2. 项类 → Term
   3. 因子类 → Factor ← Number & Expr

   这里考虑到有两种因子，我们应当分开来处理。

   • 表达式因子：实质就是表达式加括号，而括号本质上是为了区分优先级，但优先级可以由我们的语法树结构来体现，因此为了减少类，可以将这二者统一，都使用表达式Expr来存储信息。
   • 常数因子：可以单独用Number来存。

   Expr和Number都属于因子,因此可以利用面向对象的知识，创造一个Factor接口(Interface)，然后让Expr和Number实现这个接口。

2. 实现Lexer，解析出token

   通常将词法分析部分所用的类叫做Lexer，它实现了词法分析功能，并且将分析得到的信息存储到**token流中**。

   梳理一下我们需要的token类型：+ - * ( ) NUM，可以分别对这几个类型的词法单元建立token的标识符，建立一个token类来实现这个操作

   public class Token {
     public enum Type { ADD, SUB, MUL, LPAREN, RPAREN, NUM };
     private final Type type;
     private final String content;
     //....
   }

   同时，在词法分析部分，lexer需要识别不同的token，注意到，这几个类型的词法单元的开头字符必然不同，因此我们利用这一点来实现词法分析。

   public Lexer(String input) {
       int pos = 0;
       while (pos < input.length()) {
           if (input.charAt(pos) == '(') {
               tokens.add(new Token(Token.Type.LPAREN, "("));
               pos++;
           } else if (input.charAt(pos) == ')') {
               tokens.add(new Token(Token.Type.RPAREN, ")"));
               pos++;
           } else if (input.charAt(pos) == '+') {
               tokens.add(new Token(Token.Type.ADD, "+"));
               pos++;
           } else if (input.charAt(pos) == '-') {
               tokens.add(new Token(Token.Type.SUB, "-"));
               pos++;
           } else if (input.charAt(pos) == '*') {
               tokens.add(new Token(Token.Type.MUL, "*"));
               pos++;
           } else {
               char now = input.charAt(pos);
               StringBuilder sb = new StringBuilder();
               while (now >= '0' && now <= '9') {
                   sb.append(now);
                   pos++;
                   if (pos >= input.length()) {
                       break;
                   }
                   now = input.charAt(pos);
               }
               tokens.add(new Token(Token.Type.NUM, sb.toString()));
           }
       }
   }

   这样，就获得了一个经过了词法分析的token流，便可以从中逐一地拿出token方便我们进行语法分析了。

3. Parser

   首先关注给出的文法，由于表达式的解析中存在表达式的嵌套，并不能直接的使用递归下降法：否则会陷入无穷递归的情景。

   事实上，在编译原理中就有类似规则的文法叫做左递归文法，它是不能用递归下降法解决的。幸运的是，可以通过改写文法来消除左递归：

   这里，花括号代表可以有0个或多个该部分，这样的改写与我们对原本规则的理解一致，因此是等价的。类似的，我们对其他的规则也进行改写：

   至此，parser部分的关键，则是如何用获得的token判断应当如何调用解析的方法：

   public Expr parserExpr() {
     ArrayList<Term> terms = new ArrayList<>();
     ArrayList<Token> ops = new ArrayList<>();
     
     terms.add(parserTerm());
     //遇到+-则为项的终止
     while (lexer.notEnd() && 
           (lexer.now().getType() == Token.Type.ADD 
            || lexer.now().getType() == Token.Type.SUB )) {
       ops.add(lexer.now());
       lexer.move();
       terms.add(parserTerm());
     }
     
     return new Expr(terms, ops);
   }
   
   public Term parserTerm() {
     ArrayList<Factor> factors = new ArrayList<>();
     
     factors.add(parserFactor());
     //遇到*为因子的终止
     while (lexer.notEnd() && 
            lexer.now().getType() == Token.Type.MUL) {
       lexer.move();
       factors.add(parserFactor());
     }
     
     return new Term(factors);
   }
   
   public Factor parserFactor() {
     if (lexer.now().getType() == Token.Type.NUM) {
       Num num = new Num(lexer.now().getContent());
       lexer.move();
       return num;
     } else {
      // 这里调用move之前lexer.now()是(    
      lexer.move();    
      Expr expr = parserExpr();   
      // 这里调用move之前lexer.now()是)    
      lexer.move();   
      // 调用上面的move之后刚好保证表达式因子的全部成分被跳过。    
      return expr;  
     }
   }

其中，lexer.now()获取当前分析的token，lexer.move()则可以移动到下一个token。