利用元胞自动机模拟复杂网络中的信息传递

在学习网络及其存在的环境一章节时，我使用元胞自动机来对谢林模型进行了一定的探索。元胞自动机能以一种简单的方式，用数量较大的小单元来模拟复杂情景下的社会问题。

在之后的学习中，我进一步了解到了社交网络中的信息传递，对复杂网络中的信息传递，如在互联网上的信息传递产生了一定的探索兴趣。但是，社交网络具有参与人数众多、信息传递复杂的特点，难以通过直接建模对社交网络中的信息传递进行模拟。

能否使用元胞自动机对复杂网络中的信息传递进行一定的模拟？我阅读了相关文献，了解到答案是肯定的，可以使用元胞自动机来模拟复杂社交网络中的信息传递。

复杂系统

复杂系统可以认为具有两个共通的特征：由大量简单元素或主体组成、元素间存在着往往非线性的不平凡的关系。任何领域的系统只要满足了上述两点条件都可以被称为复杂系统，如大脑的神经网络、社交网络等等。在不同的场景中可以有定制的模型来描述其中的复杂性，但是是否有一种更为普适的方式来研究系统中的复杂性。

即需要一个工具，面对普遍的场景，在没有特定假设的情况下刻画系统的复杂性。信息论就可以担当这一角色：绕过复杂的非线性关系，只要能够获取概率分布，就能度量系统内发生的信息变化。这里，用信息变化反映了系统的变化，信息是广义上的信息。

系统的信息变化离不开其中的基本组成部分，将基本组成部分的信息计算称为分布式计算，指的是系统中的个体在操作和加工信息。这种由基本单元进行计算影响全体的方式是与元胞自动机的计算场景一致的，随着时间展开，根据规则可由当前元胞状态计算得出下一时刻所有元胞的状态，以得到全时间空间上的信息变化。

信息传递

信息指标可以度量系统的有序和无序，可以使用熵率来度量系统在时间演化上的不确定程度，不确定源自从底层完全确定的机理中涌现出的混沌。

统计复杂度可以透过观测数据捕捉到其背后的确定的规律。进一步的，这种复杂性度量指标可以用来量化涌现这一现象。

当复杂性指标和自组织现象高度相关的时候，就可以量化一个系统的自组织程度。统计复杂度作为一个经典的复杂性指标，已经被尝试应用在自组织量化研究上了。当前学者认为，环境会隐含地传递信息，反映在系统主体状态的概率分布及其变化里。

一个值得注意的问题是，很多信息论指标需要大量的数据才能够被准确地计算出来。针对这一问题，可以通过一些计算工具辅助，通过降维来减轻对数据量的要求，如核函数估计法和K近邻算法。

分布式计算

在复杂系统当中，每一个主体都在进行“无意识”地计算，根据某些输入，得到一些输出。这样的分布式计算在同一时刻发生在组成一个系统的所有个体身上，而且往往与主体间相互作用有关。计算的发生，带来信息的变化，可以被信息论的性质所捕获。

分布式计可以分为以下三类：信息存储、信息转移和信息修正。在下面进行详细介绍

信息存储

信息存储指的是一个变量历史信息中可以被用来预测其未来的信息量。

基本概念

研究信息存储最常见的指标便是过剩熵，度量了某一个体过去和未来若干时刻所有的交互关系，其数学表达式为

EX=lim⁡k→∞IX(k);X(k+)E_X = \lim_{k \rightarrow \infty} I_{X^{(k)} ; X^{(k+)}}

其中X(k)X^{(k)}表示的是所有变量的k阶历史变量，X(k+)X^{(k+)}表示k阶未来变量，这里的k指的是未来k个时间周期。k趋于无穷大代表着利用所有的历史信息和所有的未来信息之间的互信息。

互信息度量的是变量间的关系，而局部互信息度量的则是事件之间的关系，互信息是局部互信息的期望值，求期望的操作代表了对局部值在时间上求平均。

在实际的研究中，对所有信息进行研究的要求过于苛刻，无法利用这么多的信息，往往会使用局部过剩熵来进行表示，其公式为：

e(i,n+1)=lim⁡k→∞e(i,n+1,k)e(i,n+1) = \lim_{k \rightarrow \infty} e(i,n+1,k)

其中i表示所研究个体的编号，如在元胞自动机场景下元胞的编号；n+1表示第n+1个时刻，k则是研究的过去和未来的时间长度。

显然无法计算k→∞k \rightarrow \infty情景下的信息指标：如果k太小，则会丢失过多的信息；而如果k太大，对采样数量要求会比较高，计算压力大。需要选定一个合适的k。并且，在实际的计算中往往并不需要利用到全部信息，真正会使用的是对于下一时刻的预测会用到的信息。

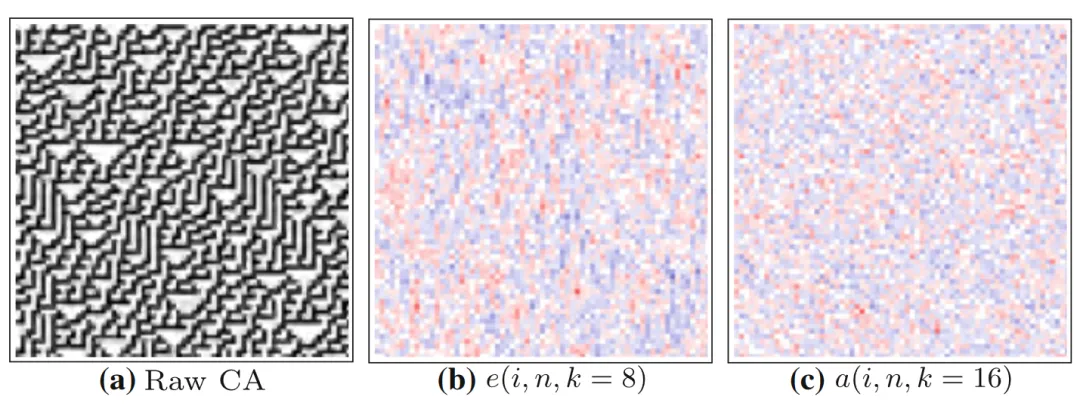
将这部分信息称之为活跃信息存储。其公式为：

AX=lim⁡k→∞AX(k)AX(k)=I(X(k);X′)A_X = \lim_{k \rightarrow \infty} A_X(k) \\ A_X(k) = I(X^{(k)};X')

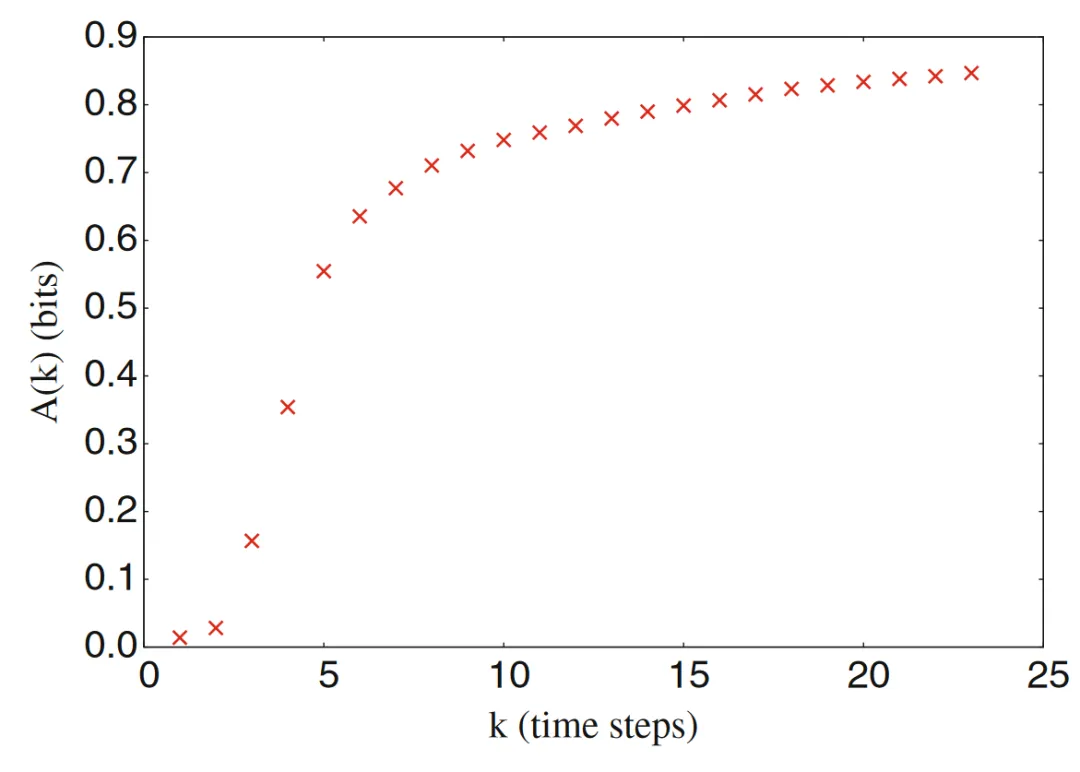
可见，随着k的取值增大，活跃信息存储应当会收敛于某一个上界，因为仅就下一时刻而言，不需要用到无穷多的信息。

如下图所示，这是元胞自动机110号中随着k增大时活跃信息存储的变化曲线。

活跃信息存储的变化曲线

元胞自动机的模拟

接下来使用元胞自动机来研究这些局部度量指标如何应用在具体场景中。

介绍一维元胞自动机中会出现的斑图：

  • 域往往作为背景在一个元胞自动机的二维时空变化图上成片成片地广泛存在。
  • 两片域之间会存在边界，被定义为粒子（particle），在有的文献中也称作域墙（domain wall）。
  • 粒子有静态和动态之分。
  • 如果随着时间展开，某粒子只在特定的几个元胞上出现，那么它就是静态的粒子，也被称作闪烁体（blinker）。
  • 如果该粒子能够向周围邻居细胞转移，那么它就是动态的，也被称作滑行体（glider）。所有这些斑图都具有周期变化的特征。

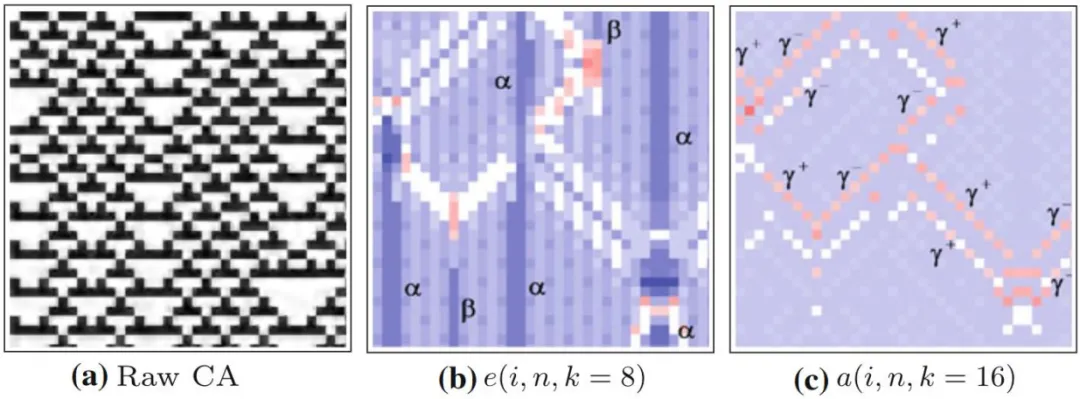
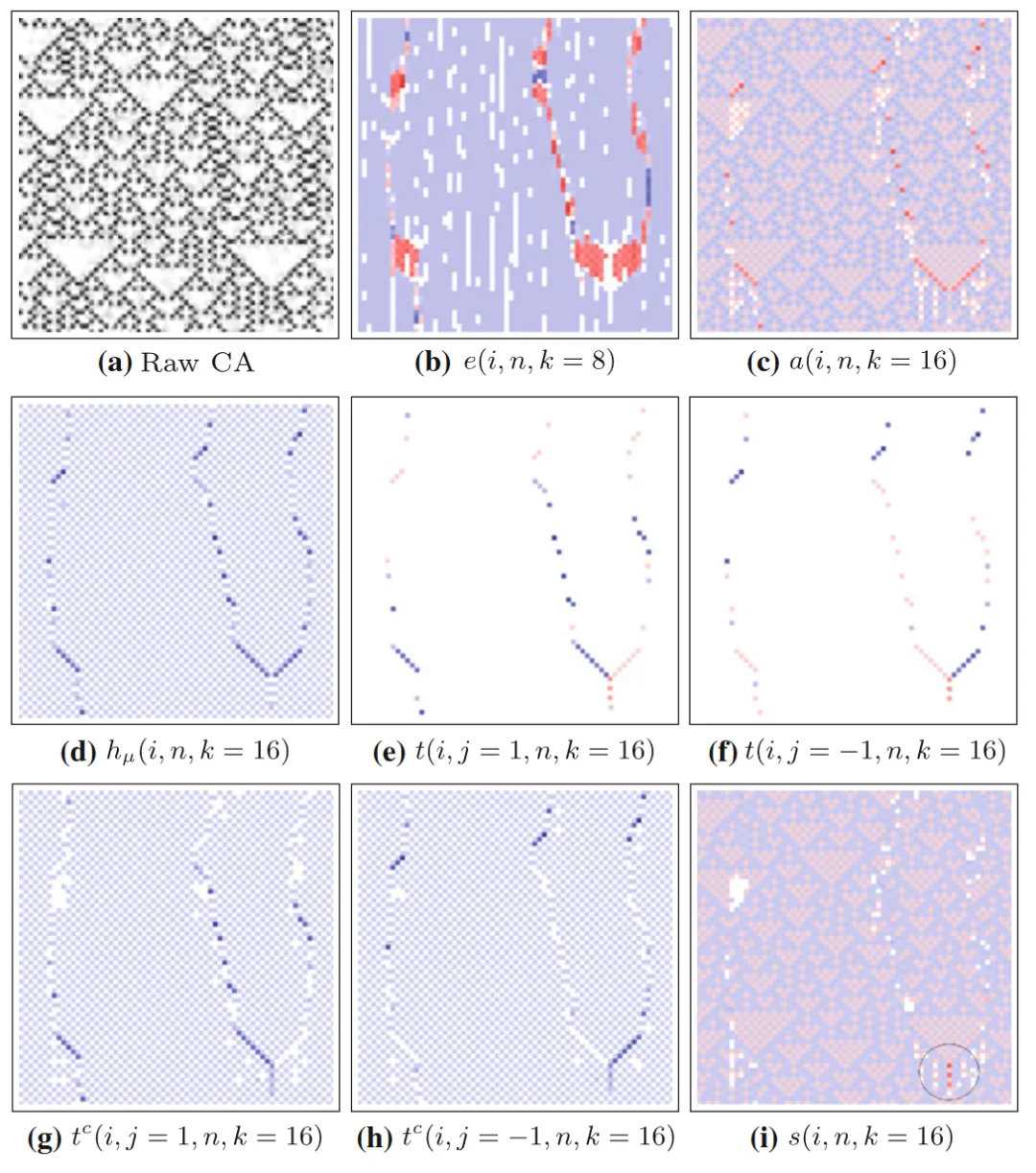
首先，研究一个采用了规则54的一维元胞自动机。横轴为空间，共有35个细胞，纵轴为时间，运行了35步

图b和c分别表示局部过剩熵和局部活跃信息存储的分布图，蓝色为正值，红色为负值。α\alpha和β\beta标记了局部过剩熵值比较大的区域，识别出的图案是闪烁体。

随着时间轴从上往下，闪烁体呈现出0−0−0−10-0-0-1的模式交替出现，而旁边呈现周期变化0−0−1−10-0-1-1和0−10-1的则是域。

活跃信息存储只能关注与下一时刻状态相关的周期规律，而局部过剩熵可以度量所有k阶未来相关的周期规律，所以度量粒子的值会更大，与其他没有粒子出现的区域区别更明显。

图片

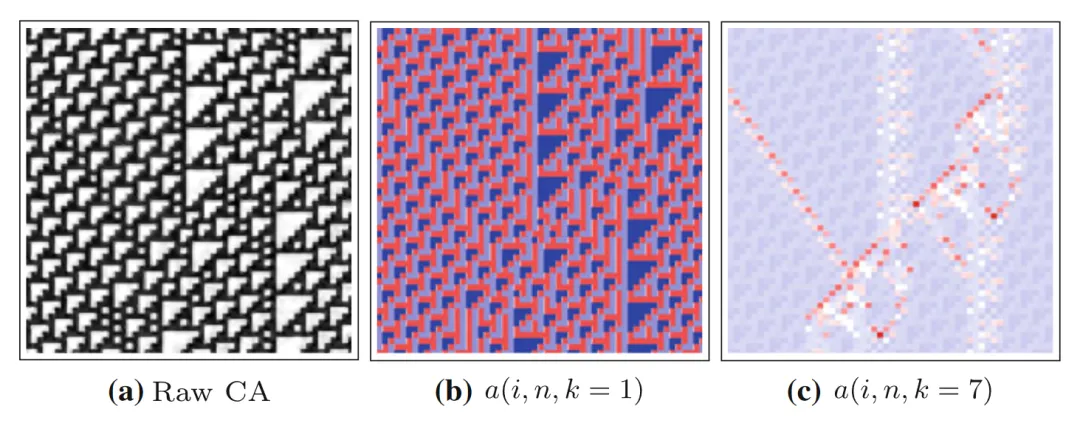
接下来我们对比一下不同k的选择会对度量结果有什么影响。下图展示了110号规则元胞自动机。相比于k=7，k=1的情况下丢失的信息更多，已经几乎无法识别出运动的粒子。

在算力支持的情况下，为了利用尽可能多的信息，应该使k尽可能大。

图片

还有一个几乎没有信息存储的过程。如下图所示的30号规则元胞自动机，局部过剩熵和局部活跃信息存储都没有呈现出清晰有指向的分布。事实上，这样的规则在分类中正属于混沌类型规则。

图片

信息转移

基本概念

信息转移是的定义是：对于信息转移的对象而言，转移到的目标信息过去没有存储在信息主体中，而在未来存储了。度量信息转移的指标采用转移熵，其数学公式为：

TY→X=lim⁡k→∞∑wnp(wn)log⁡2p(xn+1∣xn(k),yn)p(xn+1∣xn(k))T_{Y \rightarrow X} = \lim_{k \rightarrow \infty} \sum_{w_n} p(w_n) \log_2 \frac{p(x_{n+1} | x_n^{(k)},y_n)} {p(x_{n+1} | x_n^{(k)})}

该式子中，Y是信息转移的信息源主体，X是信息转移的目标主体，p(wn)p(w_n)表示(x(n+1),xn(k),yn)(x_{(n+1)},x_n^{(k)},y_n)的联合概率分布，使用联合概率分布代表了对时间的求期望操作，去除用联合概率分布求期望的操作后，计算的是局部转移熵，反映了局部时间上的信息转移指标。

局部活跃信息存储作为一种互信息是没有方向的或者说是双向的，而局部转移熵是有方向的。

上述的公式只考虑了信息转移中单一信息源对目标的影响，但在实际系统中情况往往会更为复杂，会在多个源之间会存在相互作用。

  • 如果只考虑某一个源主体转移的信息，可以来自多个信息源，则称为表面转移熵；
  • 如果想度量只来自于某一个源，不关注来自目标主体自身和其他潜在信息源的信息，则要计算的指标称为完全转移熵。
  • 如果把所有可以作为源的主体都考虑进计算，则称为集体转移熵*

在一个完全确定的系统中，如初等元胞自动机，集体转移熵就等价于熵率。这反映了，细胞下一时刻状态的不确定性来自于其自身的历史和其他细胞对它的相互作用。

元胞自动机的模拟

下图研究了一个采用18号规则和元胞自动机和各种指标的分布图。该元胞自动机研究了67个细胞的67个时间步长上的信息转移变化。

tct^c表示局部完全转移熵，t表示局部表面转移熵，j=1j=1和j=−1j=-1分别表示源主体在目标主体的左侧和右侧。

相比于局部活跃信息存储等指标，局部转移熵能更清晰地捕捉粒子的运动。事实上，对于一个运动粒子来说，局部转移熵更倾向于标记它在时间轴上最前沿的边界，因为只有在这里主要发生信息转移，而在粒子的其他区域则主要发生信息存储。

各种局部转移熵

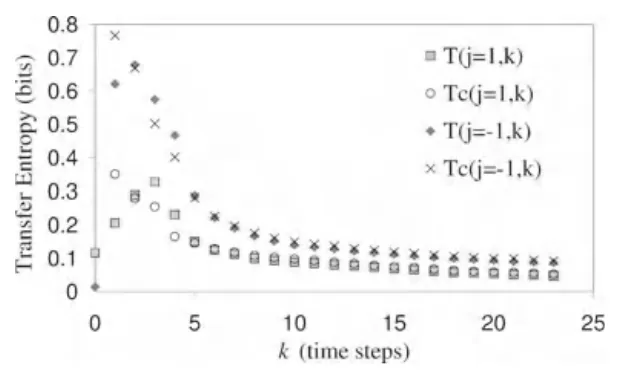
当k较小时，转移熵中有一部分信息是目标主体的历史所提供，所以为了捕捉到纯粹的信息转移，k的取值越大越好。下图是随着k的增大，各种转移熵的变化曲线。

图片

关于转移熵的应用中，有一个非常著名的概念——格兰杰因果。但是，转移熵是否真正刻画了因果关系。因果关系的刻画应当不只依赖于时间先后的区别，本质上是在问这样一个问题：如果改变了源的状态，目标的状态会在多大程度上发生改变。信息流这一指标，旨在捕获转移熵捕获不到的因果效应，其数学公式定义为：

f(a→b∣s^)=log⁡2p(b∣a^,s^)∑a′p(a′∣s^)∗p(b∣a′^,s′)f(a \rightarrow b | \hat{s}) = \log_2 \frac{p(b | \hat{a}, \hat{s})} {\sum_{a'} p(a' | \hat{s}) * p(b | \hat{a'},s')}

其中s^\hat{s}表示对s进行干预，p(y∣x^)p(y | \hat{x})表示在干预发生后的条件概率，为

p(y∣x^)=∑up(y∣x,u)p(u)p(y|\hat{x}) = \sum_u p(y |x,u) p(u)

u指的是所有会对x产生影响的变量，而通过求期望的操作，覆盖了所有可能的干预。

信息修正

基本概念

信息修正描述了从不同源传递来的信息的交互，无论传递来的信息是一种信息存储还是信息转移，而这种交互导致了修正现象的发生。在元胞自动机的图形中表现为两个粒子相撞的情景。

当两个滑行体相遇时，由于涉及到了相撞的滑行体带来的信息修正，任何一个滑行体都无法按照固有规律来准确预测下一时刻元胞的状态，局部转移熵都是负值。

使用可分离信息来识别这种信息修正，其数学表达式为：

s(i,n,k)=a(i,n,k)+∑j=−r,j≠0+rt(i,j,n,k)s(i,n,k) = a(i,n,k) + \sum^{+r}_{j=-r,j \ne 0} t(i,j,n,k)

在公式上，表现为把局部活跃信息存储和一定领域内所有源的各自的局部表面转移熵加在一起。其物理含义为：在对某一个元胞下一时刻做预测时，我们能否对所有源进行分别单独地观测。

如果s(i,n,k)是负值，就意味着所有源单独对目标提供的信息加在一起都不足以让观察者对目标做出正确的预测，要想准确预测目标主体下一时刻状态，我们必须要把所有的源作为一个整体来观测，即考虑到源与源之间的交互作用。

元胞自动机的模拟

即使是只有一个滑行体，也可能出现微弱的信息修正，即软碰撞。

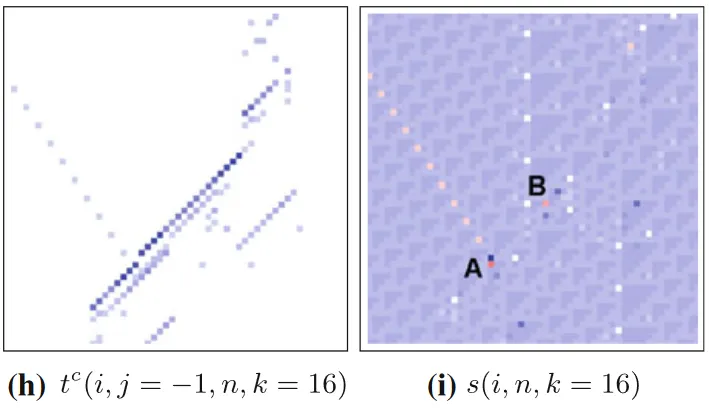
在下图所示的110号元胞自动机中，A点处有深红色点，代表着两个滑行体的硬碰撞，而在A点的左上方，有一列浅红色点。这些点在图h中可以由局部完全转移熵识别出来，是滑行体的轨迹。

图片

碰撞的发生将原先两个信息载体映射到了碰撞后的信息，无论原先的信息是什么，都有一定的信息消失了——被损毁了。

为了刻画这种不可逆的信息损毁，引入信息损毁这个指标，其在元胞自动机里的局部表达形式为：

d(i,n+1,m)=h(xi,n∣Xi,n+1,m)Xi,n+1,m=Xi+q,n+1∣∀q:−m≤q≤+md(i,n+1,m) = h(x_{i,n} | X_{i,n+1,m}) \\ X_{i,n+1,m} = {X_{i+q,n+1} | \forall q:-m \leq q \leq +m}

局部信息损毁实际上就是在算一种局部条件熵，是在已知n+1时刻某些元胞状态的条件下，求对n时刻某一个元胞状态的条件熵。也就是在问，当已知未来时，对当下状态的预测还剩余多少不确定性。这个值越大，说明信息损毁的程度越高。如果无法从输出反推出关于输入的任何信息，所以信息损毁的大小就是输入变量的熵（或事件的局部熵），即全部信息都被损毁了。

复杂系统中信息论的实际应用

元胞自动机上的斑图是体现信息动力学的重要载体。静态的粒子（闪烁体）进行着信息存储，动态的粒子（滑行体）进行着信息转移，而粒子的碰撞则是在进行信息修正。

网络和相变

把模型建模成一个网络，主体看做节点，关系看作连边，这是研究复杂系统的重要手段。著名复杂科学学者米歇尔曾指出，一个重要的挑战是理解网络上信息传播的机制，以及这些网络是如何处理和加工信息的。

连贯信息结构的进化

连贯信息结构指的是复杂系统计算中会被持续观察到的一个特征。这个概念的提出是想指代各个系统中类似于元胞自动机中滑翔体那样的结构，比如鸟群的集群行为，基因网络上的信号传播还有神经元集群中的“波”等等。

根据朗顿的分析，混沌边缘处系统会有最大的计算能力，相比于处于混沌边缘的系统过于有序的系统虽然有连贯信息结构，但结构太小；而过于混沌的系统，任何结构的连贯性都被破坏了。

观察局部转移熵的大小变化情况，不难发现这里有不同种类的连贯信息结构。有的移动快，有的移动慢，有的包含信息量多，有的包含信息量少，正如元胞自动机中也有五花八门的滑翔体。这些结构正是复杂系统实现最大计算能力的要素。

整个实验同时还发现，以每条连边转移熵最大化为目标，在某种程度上正契合复杂适应系统的进化机制。虽然拥有最大转移熵的蛇形机器人不会快速而协调的运动，但它们有足够的计算能力，使得它们在充满挑战的环境中找到正确的方位。

把局部转移熵应用在了生物学系统上，发现局部转移熵相比于以往计算平均值来说可以揭示更多有意思的洞见。目前已有的实验对象包括睡眠呼吸暂停、大脑中的层次结构以及蛇形机器人的进化，可见复杂系统中的信息动力学的应用普适性。

参考文献

1
2
3
4
5
6
7
8
9
[1] Lizier, J. T. (2013). The Local Information Dynamics of Distributed Computation in Complex Systems (Springer Theses). Springer Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-32952-4

[2] 杨明哲. (2024-01-30). 复杂系统研究为什么关注信息论？. https://mp.weixin.qq.com/s?__biz=MzIzMjQyNzQ5MA==&mid=2247682183&idx=1&sn=d4de323f6922df4022dc5f9d4bc3ccb2&chksm=e899520adfeedb1c0063f050efb19fd223e3829869911b9c34c6ce243177746dd973ac1351ef&scene=21#wechat_redirect

[3] 杨明哲. (2024-03-28). 三种信息动力学：如何识别元胞自动机中的涌现？.  https://mp.weixin.qq.com/s?__biz=MzIzMjQyNzQ5MA==&mid=2247687488&idx=1&sn=94317200cb17686949f63b9f65d87ced&chksm=e89947cddfeecedb962d2a3977a0b254d4c41c2b37a3fcb5ca03d4cd8bc250ba46c4ef622222&scene=21#wechat_redirect

[4] Mediano, P. A. M., Rosas, F., Carhart-Harris, R. L., Seth, A. K., & Barrett, A. B. (2019). Beyond integrated information: A taxonomy of information dynamics phenomena (arXiv:1909.02297). arXiv. http://arxiv.org/abs/1909.02297

[5] M. Prokopenko, F. Boschietti, A.J. Ryan, An information-theoretic primer on complexity, self-organization, and emergence. Complexity 15(1), 11–28 (2009)